Równania jednorodne (zadania)

Przed przystąpieniem do rozwiązywania zadań warto zajrzeć do zakładki Teoria tutaj.

Zadanie 1. Rozwiąż równania jednorodne:

1) $\dpi{120} y'=\frac{y}{x}+\sin \frac{y}{x}$

Rozwiązanie

Wykonujemy podstawienie:

$\dpi{120} \frac{y}{x}=t$

$\dpi{120} y=tx$

$\dpi{120} y'=t'x+t$

Wstawiamy do równania:

$\dpi{120} t'x+t=t+\sin t$

$\dpi{120} t'x=\sin t/:x\sin t,\; \sin t\neq 0\Rightarrow t\neq 0+k\pi ,k\in Z$

$\dpi{120} \frac{1}{\sin t}\cdot t'=\frac{1}{x}$

Wstawiamy $\dpi{120} t'=\frac{dt}{dx}$ :

$\dpi{120} \frac{1}{\sin t}\cdot \frac{dt}{dx}=\frac{1}{x}$

$\dpi{120} \frac{1}{\sin t}dt=\frac{1}{x}dx$

Całkujemy stronami:

$\dpi{120} \int \frac{1}{\sin t}dt=\int \frac{1}{x}dx$

Wykorzystujemy wzór na całkę po lewej stronie równania $\dpi{120} \int \frac{dx}{\sin x}=\ln \left | tg\frac{x}{2} \right |+c$ . Mamy:

$\dpi{120} \ln \left | tg\frac{t}{2} \right |=\ln \left | x \right |+c_{1},\; c_{1}\in R$

Stałą zapisujemy jako $\dpi{120} c_{1}=\ln c_{2},\; c_{2}\in R_{+}$ .

$\dpi{120} \ln \left | tg\frac{t}{2} \right |=\ln \left | x \right |+\ln c_{2}$

Z własności $\dpi{120} \ln x+\ln y=\ln \left (xy \right )$ otrzymujemy:

$\dpi{120} \ln \left | tg\frac{t}{2} \right |=\ln c_{2}\left | x \right |$

$\dpi{120} \left | tg\frac{t}{2} \right |= c_{2}\left | x \right |$

Opuszczamy wartość bezwzględną i dołączamy rozwiązanie $\dpi{120} t=0+k\pi$ mamy:

$\dpi{120} tg\frac{t}{2} = c\left | x \right |,\; c\in R$

$\dpi{120} \frac{t}{2}=arc\, tg\, c\left | x \right |$

$\dpi{120} t=2arc\, tg\, c\left | x \right |$

Wracamy do podstawienia $\dpi{120} t=\frac{y}{x}$ . Mamy:

$\dpi{120} \frac{y}{x}=2arc\, tg\, c\left | x \right |,\; c\in R$

$\dpi{120} y=2x\cdot arc\, tg\, c\left | x \right |,\; c\in R$

Jest to końcowe rozwiązanie.

Pokaż rozwiązanie

Zwiń

2) $\dpi{120} y'=\frac{y+x}{y-x}$

Rozwiązanie

Najpierw musimy doprowadzić funkcję po prawej stronie równania do postaci $\dpi{120} \varphi \left ( \frac{y}{x} \right )$ :

$\dpi{120} \frac{y+x}{y-x}=\frac{x\left ( \frac{y}{x} +1\right )}{x\left ( \frac{y}{x}-1 \right )}=\frac{\frac{y}{x}+1}{\frac{y}{x}-1}$

Równanie różniczkowe przyjmie postać:

$\dpi{120} y'=\frac{\frac{y}{x}+1}{\frac{y}{x}-1}$

Wykonujemy podstawienie:

$\dpi{120} \frac{y}{x}=t$

$\dpi{120} y=tx$

$\dpi{120} y'=t'x+t$

Wstawiamy do równania:

$\dpi{120} t'x+t=\frac{t+1}{t-1}$

$\dpi{120} t'x=\frac{t+1}{t-1}-t$

Sprowadzamy do wspólnego mianownika:

$\dpi{120} t'x=\frac{t+1-t^{2}+t}{t-1}$

$\dpi{120} t'x=\frac{-t^{2}+2t+1}{t-1}$

Jest to równanie o rozdzielonych zmiennych:

$\dpi{120} t'x=\frac{-t^{2}+2t+1}{t-1}/:\frac{-t^{2}+2t+1}{t-1}\cdot x$ przy założeniu, że $\dpi{100} -t^{2}+2t+1\neq 0\Rightarrow t\neq 1+\sqrt{2},\: t\neq 1-\sqrt{2}$

$\dpi{120} \frac{t-1}{-t^{2}+2t+1}\cdot t'=\frac{1}{x}$

Wstawiamy $\dpi{120} t'=\frac{dt}{dx}$ :

$\dpi{120} \frac{t-1}{-t^{2}+2t+1}\cdot \frac{dt}{dx}=\frac{1}{x}$

$\dpi{120} \frac{t-1}{-t^{2}+2t+1}dt=\frac{1}{x}dx$

Całkujemy stronami:

$\dpi{120} \int \frac{t-1}{-t^{2}+2t+1}dt=\int \frac{1}{x}dx$

Zauważmy, że w całce po lewej stronie równania pochodna mianownika wynosi $\dpi{120} -2t+2=-2\left ( t-1 \right )$ . Zatem całkę tą możemy zapisać jako:

$\dpi{120} \int \frac{t-1}{-t^{2}+2t+1}dt=-\frac{1}{2}\int \frac{2\left ( t-1 \right )}{-t^{2}+2t+1}dt$

Korzystamy ze wzoru całkowego $\dpi{120} \int \frac{f'\left ( x \right )}{f\left ( x \right )}dx=\ln \left |f\left ( x \right ) \right |+c$ . Zatem:

$\dpi{120} \int \frac{t-1}{-t^{2}+2t+1}dt=-\frac{1}{2}\ln \left |-t^{2}+2t+1 \right | +c$

Wracając do równania otrzymujemy:

$\dpi{120} -\frac{1}{2}\ln \left |-t^{2}+2t+1 \right | =\ln \left | x \right |+c/\cdot \left ( -2 \right )$

$\dpi{120} \ln \left |-t^{2}+2t+1 \right | =-2\ln \left | x \right |+c_{1}$

$\dpi{120} \ln \left |-t^{2}+2t+1 \right | =\ln \frac{1}{x^{2}} +c_{1},\; \; c_{1}=\ln c_{2},\, c_{2}>0$

$\dpi{120} \ln \left |-t^{2}+2t+1 \right | =\ln \frac{1}{x^{2}} +\ln c_{2}$

$\dpi{120} \ln \left |-t^{2}+2t+1 \right | =\ln \frac{c_{2}}{x^{2}}$

$\dpi{120} \left |-t^{2}+2t+1 \right | =\frac{c_{2}}{x^{2}}$

$\dpi{120} -t^{2}+2t+1 =\frac{c_{3}}{x^{2}},\; c_{3}\in R-\left \{ 0 \right \}$

Dla $\dpi{120} c_{3}=0$ otrzymujemy rozwiązania, które odrzuciliśmy przedtem w założeniach $\dpi{120} t=1+\sqrt{2}$ i $\dpi{120} t=1-\sqrt{2}$ . Dołączamy je teraz, a to wiąże się z kolejną zmianą stałej. Otrzymujemy:

$\dpi{120} -t^{2}+2t+1 =\frac{c_{4}}{x^{2}},\; c_{4}\in R$

Wracamy do podstawienia $\dpi{120} t=\frac{y}{x}$ . Mamy:

$\dpi{120} -\frac{y^{2}}{x^{2}}+2\cdot \frac{y}{x}+1=\frac{c_{4}}{x^{2}}/\cdot x^{2}$

$\dpi{120} -y^{2}+2xy+x^{2}=c_{4},\; c_{4}\in R$

To jest nasze końcowe rozwiązanie.

Pokaż rozwiązanie

Zwiń

3) $\dpi{120} y'=\frac{y+x}{x-y}$

Rozwiązanie

Najpierw musimy doprowadzić funkcję po prawej stronie równania do postaci $\dpi{120} \varphi \left ( \frac{y}{x} \right )$ :

$\dpi{120} \frac{y+x}{x-y}=\frac{x\left ( \frac{y}{x} +1\right )}{x\left ( 1-\frac{y}{x} \right )}=\frac{\frac{y}{x}+1}{1-\frac{y}{x}}$

Równanie różniczkowe przyjmie postać:

$\dpi{120} y'=\frac{\frac{y}{x}+1}{1-\frac{y}{x}}$

Wykonujemy podstawienie:

$\dpi{120} \frac{y}{x}=t$

$\dpi{120} y=tx$

$\dpi{120} y'=t'x+t$

Wstawiamy do równania:

$\dpi{120} t'x+t=\frac{t+1}{1-t}$

$\dpi{120} t'x=\frac{t+1}{1-t}-t$

Sprowadzamy do wspólnego mianownika:

$\dpi{120} t'x=\frac{t+1-t+t^{2}}{1-t}$

$\dpi{120} t'x=\frac{t^{2}+1}{1-t}$

Jest to równanie o rozdzielonych zmiennych:

$\dpi{120} t'x=\frac{t^{2}+1}{1-t}/:\frac{t^{2}+1}{1-t}\cdot x$

$\dpi{120} \frac{1-t}{t^{2}+1}\cdot t'=\frac{1}{x}$

Wstawiamy $\dpi{120} t'=\frac{dt}{dx}$ :

$\dpi{120} \frac{1-t}{t^{2}+1}\cdot \frac{dt}{dx}=\frac{1}{x}$

$\dpi{120} \frac{1-t}{t^{2}+1}dt=\frac{1}{x}dx$

Całkujemy stronami:

$\dpi{120} \int \frac{1-t}{t^{2}+1}dt=\int \frac{1}{x}dx$

Zauważmy, że całkę po lewej stronie równania możemy zapisać jako sumę dwóch całek:

$\dpi{120} \int \frac{1-t}{t^{2}+1}dt=\int \frac{1}{t^{2}+1}dt-\int \frac{t}{t^{2}+1}dt=\int \frac{1}{t^{2}+1}dt-\frac{1}{2}\int \frac{2t}{t^{2}+1}dt=$

$\dpi{120} =arctg\, t -\frac{1}{2}\ln \left ( t^{2}+1 \right )+c_{1}$

Wykorzystaliśmy wzór całkowy $\dpi{120} \int \frac{f'\left ( x \right )}{f\left ( x \right )}dx=\ln \left |f\left ( x \right ) \right |+c$ . Wracając do równania otrzymujemy:

$\dpi{120} arctg\, t -\frac{1}{2}\ln \left ( t^{2}+1 \right )=\ln \left | x \right |+c,\; c\in R$

Wracamy do podstawienia $\dpi{120} t=\frac{y}{x}$ . Mamy:

$\dpi{120} arctg\, \frac{y}{x} -\frac{1}{2}\ln \left ( \frac{y^{2}}{x^{2}}+1 \right )=\ln \left | x \right |+c,\; c\in R$

To jest nasze końcowe rozwiązanie.

Pokaż rozwiązanie

Zwiń

Zadanie 2. Rozwiąż równania jednorodne z warunkami początkowymi:

1) $\dpi{120} xy'=y\left ( 1+\ln y- \ln x\right ),\; y\left ( 1 \right )=e^{-\frac{1}{2}}$

Rozwiązanie

$\dpi{120} xy'=y\left ( 1+\ln y- \ln x\right )/:x$

$\dpi{120} y'=\frac{y}{x}\left ( 1+\ln y- \ln x\right )$

Korzystamy z własności logarytmów $\dpi{120} \ln x-\ln y=\ln \frac{x}{y}$ . Otrzymujemy:

$\dpi{120} y'=\frac{y}{x}\left ( 1+\ln \frac{y}{x}\right )$

Wykonujemy podstawienie:

$\dpi{120} \frac{y}{x}=t$

$\dpi{120} y=tx$

$\dpi{120} y'=t'x+t$

Wstawiamy do równania:

$\dpi{120} t'x+t=t\left ( 1+\ln t \right )$

$\dpi{120} t'x=t+t\ln t-t$

$\dpi{120} t'x=t\ln t/:t\ln t\cdot x,\; t\neq 0,\: \ln t\neq 0\Rightarrow t\neq 1$

$\dpi{120} \frac{1}{t\ln t}\cdot t'=\frac{1}{x}$

Wstawiamy $\dpi{120} t'=\frac{dt}{dx}$ :

$\dpi{120} \frac{1}{t\ln t}\cdot \frac{dt}{dx}=\frac{1}{x}$

$\dpi{120} \frac{1}{t\ln t}dt=\frac{1}{x}dx$

Całkujemy stronami:

$\dpi{120} \int \frac{1}{t\ln t}dt=\int \frac{1}{x}dx$

Liczymy całkę po lewej stronie przez podstawienie:

$\dpi{120} \ln t=s$

$\dpi{120} \frac{1}{t}dt=ds$

Zatem:

$\dpi{120} \int \frac{1}{t\ln t}dt=\int \frac{1}{s}ds=\ln \left | s \right |+c_{1}=\ln \left | \ln t \right |+c_{2}$

Wracając do równania:

$\dpi{120} \ln \left | \ln t \right |=\ln \left | x \right |+c_{3}, \; c_{3}=\ln c_{4},\: c_{4}\in R_{+}$

$\dpi{120} \ln \left | \ln t \right |=\ln \left | x \right |+\ln c_{4}$

$\dpi{120} \ln \left | \ln t \right |=\ln c_{4}\left | x \right |$

$\dpi{120} \left | \ln t \right |=c_{4}\left | x \right |$

$\dpi{120} \ln t=c_{5}\left | x \right |,\; c_{5}\in R-\left \{ 0 \right \}$

Dla $\dpi{120} c_{5}=0$ otrzymujemy rozwiązanie $\dpi{120} t=1$ , które wcześniej odrzuciliśmy w założeniach. Mamy:

$\dpi{120} \left\{\begin{matrix} \ln t=c\left | x \right |,\: c\in R\\ t=0\; \; \; \; \; \;\; \; \; \; \; \; \; \; \; \; \; \end{matrix}\right.$

Wracamy do podstawienia $\dpi{120} t=\frac{y}{x}$ . Mamy:

$\dpi{120} \left\{\begin{matrix} \ln \frac{y}{x}=c\left | x \right |,\: c\in R\\ \frac{y}{x}=0\Rightarrow y=0 \; \; \;\; \; \; \end{matrix}\right.$

Uwzględniamy warunek początkowy $\dpi{120} y\left ( 1 \right )=e^{-\frac{1}{2}}$ . Otrzymujemy:

$\dpi{120} \ln \frac{e^{-\frac{1}{2}}}{1}=c\cdot \left | 1 \right |$

$\dpi{120} c=\ln e^{-\frac{1}{2}}$

$\dpi{120} c=-\frac{1}{2}$

Zatem rozwiązanie ma postać:

$\dpi{120} \ln \frac{y}{x}=-\frac{1}{2}\cdot \left | x \right |$

Pokaż rozwiązanie

Zwiń

2) $\dpi{120} y'=\frac{y}{x}-e^{\frac{y}{x}},\; \; y\left ( 1 \right )=-1$

Rozwiązanie

Wykonujemy podstawienie:

$\dpi{120} \frac{y}{x}=t$

$\dpi{120} y=tx$

$\dpi{120} y'=t'x+t$

Wstawiamy do równania:

$\dpi{120} t'x+t=t-e^{t}$

$\dpi{120} t'x=-e^{t}/:x e^{t}$

$\dpi{120} \frac{1}{e^{t}}\cdot t'=-\frac{1}{x}$

Wstawiamy $\dpi{120} t'=\frac{dt}{dx}$ :

$\dpi{120} \frac{1}{e^{t}}\cdot \frac{dt}{dx}=-\frac{1}{x}$

$\dpi{120} \frac{1}{e^{t}}dt=-\frac{1}{x}dx$

Całkujemy stronami:

$\dpi{120} \int \frac{1}{e^{t}}dt=-\int \frac{1}{x}dx$

Liczymy całkę po lewej stronie:

$\dpi{120} \int \frac{1}{e^{t}}dt=\int e^{-t}dt=-e^{-t}+c$

Wracając do równania:

$\dpi{120} -e^{-t}=-\ln \left | x \right |+c_{1},\; c_{1}\in R$

$\dpi{120} e^{-t}=\ln \left | x \right |+c,\; c\in R$

Wracamy do podstawienia $\dpi{120} t=\frac{y}{x}$ . Mamy:

$\dpi{120} e^{-\frac{y}{x}}=\ln \left | x \right |+c,\; c\in R$

Uwzględniamy warunek początkowy $\dpi{120} y\left ( 1 \right )=-1$ . Otrzymujemy:

$\dpi{120} e^{-\frac{-1}{1}}=\underset{=0}{\underbrace{\ln \left | 1 \right |}}+c$

$\dpi{120} c=e$

Zatem rozwiązanie ma postać:

$\dpi{120} e^{-\frac{y}{x}}=\ln \left | x \right |+e$

Pokaż rozwiązanie

Zwiń

3) $\dpi{120} y'=\frac{y}{x}+\cos ^{2}\frac{y}{x},\; y\left ( 1 \right )=\frac{\pi }{4}$

Rozwiązanie

Wykonujemy podstawienie:

$\dpi{120} \frac{y}{x}=t$

$\dpi{120} y=tx$

$\dpi{120} y'=t'x+t$

Wstawiamy do równania:

$\dpi{120} t'x+t=t+\cos ^{2}t$

$\dpi{120} t'x=\cos ^{2}t/:x\cdot \cos ^{2}t,\; \; \cos ^{2}t\neq 0\Rightarrow t\neq \frac{\pi }{2}+k\pi ,k\in Z$

$\dpi{120} \frac{1}{\cos ^{2}t}\cdot t'=\frac{1}{x}$

Wstawiamy $\dpi{120} t'=\frac{dt}{dx}$ :

$\dpi{120} \frac{1}{\cos ^{2}t}\cdot \frac{dt}{dx}=\frac{1}{x}$

$\dpi{120} \dpi{120} \frac{1}{\cos ^{2}t}dt=\frac{1}{x}dx$

Całkujemy stronami:

$\dpi{120} \int \frac{1}{\cos ^{2}t}dt=\int \frac{1}{x}dx$

$\dpi{120} tg\, t=\ln \left | x \right |+c,\; c\in R$

Wracamy do podstawienia $\dpi{120} t=\frac{y}{x}$ . Mamy:

$\dpi{120} tg\, \frac{y}{x}=\ln \left | x \right |+c,\; c\in R$

Uwzględniamy warunek początkowy $\dpi{120} y\left ( 1 \right )=\frac{\pi }{4}$ . Otrzymujemy:

$\dpi{120} tg\, \frac{\frac{\pi }{4}}{1}=\ln \left | 1\right |+c,\; c\in R$

$\dpi{120} c=1$

Zatem rozwiązanie ma postać:

$\dpi{120} tg\, \frac{y}{x}=\ln \left | x \right |+1$

Pokaż rozwiązanie

Zwiń

Zadanie 3. Znaleźć krzywe, dla których długość rzutu odcinka stycznej do punktu przecięcia z osią odciętych na oś odciętych jest równa sumie rzędnej i odciętej punktu styczności.

Rozwiązanie

Najpierw wykonajmy rysunek pomocniczy.

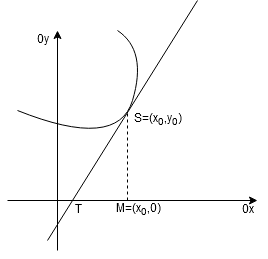
Niech $\dpi{120} S=\left ( x_{0} ,y_{0}\right )$ będzie dowolnym punktem na krzywej $\dpi{120} y=f\left ( x \right )$ . Poprowadźmy styczną do krzywej $\dpi{120} y=f\left ( x \right )$ w punkcie $\dpi{120} S=\left ( x_{0} ,y_{0}\right )$ . Równanie stycznej ma postać:

$\dpi{120} y-y_{0}=y'\left ( x-x_{0} \right )$

Obliczmy współrzędne punktu $\dpi{120} T$ . Jest to miejsce zerowe stycznej, a więc podstawiamy do równania stycznej $\dpi{120} y=0$ .

$\dpi{120} 0-y_{0}=y'\left ( x-x_{0} \right )$

$\dpi{120} -y_{0}=y'x-y'x_{0}$

$\dpi{120} y'x=-y_{0}+y'x_{0}/:y'$

$\dpi{120} x=-\frac{y_{0}}{y'}+x_{0}$

Zatem punkt $\dpi{120} T$ ma współrzędne $\dpi{120} T=\left ( -\frac{y_{0}}{y'}+x_{0},0 \right )$ . Długość rzutu odcinka stycznej do punktu przecięcia z osią odciętych na oś odciętych to $\dpi{120} \left | TM \right |$ . Mamy:

$\dpi{120} \left | TM \right |=\left | x_{0}+\frac{y_{0}}{y'}-x_{0} \right |=\left | \frac{y_{0}}{y'} \right |$

Pomijamy wartość bezwzględną (zakładając, że $\dpi{120} y_{0}>0$ ). Otrzymujemy równanie różniczkowe odpowiadające warunkom zadania:

$\dpi{120} \frac{y_{0}}{y'}=x_{0}+y_{0}$

Pomijamy dla wygody wskaźniki $\dpi{120} 0$ przy $\dpi{120} x$ i $\dpi{120} y$ . Mamy:

$\dpi{120} \frac{y}{y'}=x+y$

Przekształcamy równanie tak, aby pochodna znalazła się w liczniku.

$\dpi{120} \frac{y'}{y}=\frac{1}{x+y}/\cdot y$

$\dpi{120} y'=\frac{y}{x+y}$

Jest to równanie jednorodne. Należy je jeszcze raz przekształcić, aby było to wyraźnie widoczne.

$\dpi{120} y'=\frac{x\cdot \frac{y}{x}}{x\cdot \left (1+\frac{y}{x} \right )}$

$\dpi{120} y'=\frac{\frac{y}{x}}{1+\frac{y}{x}}$

Wykonujemy podstawienie:

$\dpi{120} \frac{y}{x}=t$

$\dpi{120} y=tx$

$\dpi{120} y'=t'x+t$

Wstawiamy do równania:

$\dpi{120} t'x+t=\frac{t}{1+t}$

$\dpi{120} t'x=\frac{t}{1+t}-t$

$\dpi{120} t'x=\frac{t-t-t^{2}}{1+t}$

$\dpi{120} t'x=\frac{-t^{2}}{1+t}$

$\dpi{120} \frac{1+t}{t^{2}}\cdot t'=-\frac{1}{x}$

Wstawiamy $\dpi{120} t'=\frac{dt}{dx}$ :

$\dpi{120} \frac{1+t}{t^{2}}\cdot \frac{dt}{dx}=-\frac{1}{x}$

$\dpi{120} \frac{1+t}{t^{2}}dt=-\frac{1}{x}dx$

Całkujemy stronami:

$\dpi{120} \int \frac{1+t}{t^{2}}dt=-\int \frac{1}{x}dx$

Liczymy całkę po lewej stronie równania:

$\dpi{120} \int \frac{1+t}{t^{2}}dt=\int \frac{1}{t^{2}}dt+\int \frac{1}{t}dt=-\frac{1}{t}+\ln \left | t \right |$

Wracając do równania mamy:

$\dpi{120} -\frac{1}{t}+\ln \left | t \right |=-\ln \left | x \right |+c_{1},\; c_{1}\in R$

$\dpi{120} -\frac{1}{t}=-\ln \left | x \right |-\ln \left | t \right |+c_{1}/\cdot \left ( -1 \right )$

$\dpi{120} \frac{1}{t}=\ln \left | x \right |+\ln \left | t \right |+c_{2},\; c_{2}\in R$

Stałą $\dpi{120} c_{2}$ zapisujemy w postaci $\dpi{120} c_{2}=\ln c_{3},\; c_{3}\in R_{+}$ .

$\dpi{120} \frac{1}{t}=\ln \left | x \right |+\ln \left | t \right |+\ln c_{3}$

$\dpi{120} \frac{1}{t}=\ln c_{3}\left | xt \right |$

$\dpi{120} c_{3}\left | xt \right |=e^{\frac{1}{t}}$

$\dpi{120} xt=ce^{\frac{1}{t}},\; c\in R$

Wracamy do podstawienia $\dpi{120} t=\frac{y}{x}$ . Mamy:

$\dpi{120} x\cdot \frac{y}{x}=ce^{\frac{1}{\frac{y}{x}}},\; c\in R$

$\dpi{120} y=ce^{\frac{x}{y}},\; c\in R$

Równanie $\dpi{120} y=ce^{\frac{x}{y}},\; c\in R$ reprezentuje rodzinę krzywych spełniających warunki zadania.

Pokaż rozwiązanie

Zwiń