Współrzędne biegunowe (teoria)

W przypadku, gdy obszar całkowania $\dpi{120} D$ jest kołem, wycinkiem koła, pierścieniem lub wycinkiem pierścienia wygodnie jest nam wprowadzić tzw. współrzędne biegunowe. Można je używać również przy innych obszarach, ale te pojawiają się najczęściej na studiach.

Wzory przejścia od współrzędnych $\dpi{120} x,y$ do współrzędnych biegunowych $\dpi{120} r,\varphi$ :

$\dpi{120} x=r\cos \varphi$

$\dpi{120} y=r\sin \varphi$

Całka podwójna we współrzędnych biegunowych wyraża się wzorem:

$\dpi{120} \underset{D\; \; \; \; }{\iint_{\, }^{\, }}f\left ( x,y \right )dxdy=\underset{\Omega \; \; \; \; }{\iint_{\, }^{\, }}f\left ( r\cos \varphi ,r\sin \varphi \right )\cdot {\color{Red} r}\, d\varphi dr$

gdzie $\dpi{120} \Omega$ jest zbiorem wartości $\dpi{120} \left ( r,\varphi \right )$ przyporządkowanych punktom $\dpi{120} \left (x,y \right )$ zbioru $\dpi{120} D$ .

Pamiętajmy o czynniku $\dpi{120} {\color{Red} r}$ znajdującym się pod całką. Jest to tzw. jakobian przekształcenia.

Przykłady najczęściej występujących obszarów, w których wprowadzamy współrzędne biegunowe:

1. $\dpi{120} x^{2}+y^{2}\leqslant R^{2}$ – koło o środku w punkcie $\dpi{120} \left (0,0 \right )$ i promieniu $\dpi{120} R$ zapiszemy we współrzędnych biegunowych jako:

$\dpi{120} K\left ( \left ( 0,0 \right ) ,R\right )=\left \{ 0\leqslant r\leqslant R,\; 0\leqslant \varphi \leqslant 2\pi \right \}$

2. $\dpi{120} x^{2}+y^{2}\leqslant R^{2},\; x\leqslant 0,\; y\leqslant 0$ – ćwiartka koła

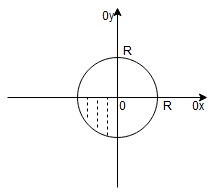
o środku w punkcie $\dpi{120} \left (0,0 \right )$ i promieniu $\dpi{120} R$ zapiszemy we współrzędnych biegunowych jako:

$\dpi{120} 0\leqslant r\leqslant R,\; \pi \leqslant \varphi \leqslant \frac{3}{2}\pi$

3. $\dpi{120} \left (R_{1} \right )^{2}\leqslant x^{2}+y^{2}\leqslant \left (R_{2} \right )^{2}$ – pierścień kołowy

pierścień kołowy

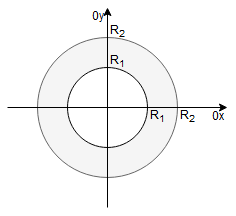
zapiszemy we współrzędnych biegunowych jako:

$\dpi{120} R_{1}\leqslant r\leqslant R_{2},\; 0 \leqslant \varphi \leqslant 2\pi$

4. $\dpi{120} \left (R_{1} \right )^{2}\leqslant x^{2}+y^{2}\leqslant \left (R_{2} \right )^{2},\; x\leqslant 0,\; y\geqslant 0$ – ćwiartka pierścienia kołowego

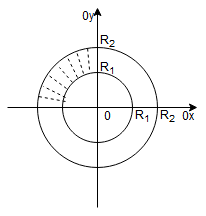
zapiszemy we współrzędnych biegunowych jako:

$\dpi{120} R_{1}\leqslant r\leqslant R_{2},\; \frac{\pi }{2} \leqslant \varphi \leqslant \pi$

5. $\dpi{120} x^{2}+y^{2}\leqslant R^{2},\; 0\leqslant y\leqslant x$ – wycinek koła

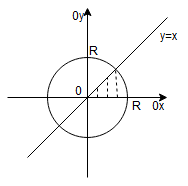
zapiszemy we współrzędnych biegunowych jako:

$\dpi{120} 0\leqslant r\leqslant R,\; 0 \leqslant \varphi \leqslant \frac{\pi}{4}$

Widzimy na podstawie powyższych przykładów, że $\dpi{120} r$ jest zakresem zmienności długości promienia, zaś $\dpi{120} \varphi$ zakresem zmienności kąta licząc od dodatniej osi $\dpi{120} 0x$ .

Zapraszamy do zadań! tutaj