Współrzędne biegunowe (zadania)

Mamy 3 zadania. Zadanie 1 jest to typowe liczenie całek podwójnych z zastosowaniem współrzędnych biegunowych. Pojawiają się tutaj standardowe obszary całkowania odpowiednie dla tego typu całek. Zadanie 2 i 3 są zastosowaniem całek podwójnych do liczenia objętości figur. Zadanie 2 trochę łatwiejsze, gdyż z zapisu figury widać zarówno obszar całkowania jak i funkcję podcałkową, potrzebne do wzoru na objętość. W zadaniu 3 nie widzimy od razu tych dwu rzeczy. Pokażemy jak je znaleźć. Nie zawsze należy użyć współrzędnych biegunowych. Warto zajrzeć do zakładki Teoria tutaj.

Zadanie 1. Obliczyć za pomocą współrzędnych biegunowych całki podwójne:

1) $\dpi{120} \underset{D\; \; \; \; }{\iint_{\, }^{\, }}\left ( x^{2}+y^{2} \right )d\sigma ,\; \; D:\left \{ x^{2}+y^{2} \leqslant 1\right \}$ ,

Rozwiązanie

Naszym obszarem całkowania jest koło o środku w punkcie $\dpi{120} \left ( 0,0 \right )$ i promieniu $\dpi{120} r=1$ .

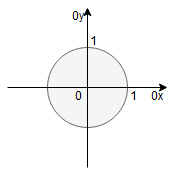
Wprowadzamy zatem współrzędne biegunowe:

$\dpi{120} x=r\cos \varphi$

$\dpi{120} y=r\sin \varphi$

Pamiętajmy o jakobianie, czyli dla współrzędnych biegunowych: $\dpi{120} {\color{Red} J=r}$ .

Ponieważ naszym obszarem całkowania jest koło (jak wyżej), więc zakres zmienności $\dpi{120} r$ oraz $\dpi{120} \varphi$ jest następujący:

$\dpi{120} 0\leqslant r\leqslant 1$ – długość promienia

$\dpi{120} 0\leqslant \varphi \leqslant 2\pi$ – mamy pełne koło

Wstawiamy współrzędne biegunowe do wyjściowej całki za $\dpi{120} x$ i za $\dpi{120} y$ , pamiętając o jakobianie. Ponieważ granice całkowania $\dpi{120} r$ i $\dpi{120} \varphi$ są stałe, więc kolejność całkowania jest dowolna, pamiętajmy jedynie o poprawnej kolejności różniczek. Zatem:

$\dpi{120} \underset{D\; \; \; \; }{\iint_{\, }^{\, }}\left ( x^{2}+y^{2} \right )d\sigma =\int_{0}^{2\pi }\int_{0}^{1}\left [ \left (\overset{x}{\overbrace{r\cos \varphi }} \right ) ^{2}+\left ( \overset{y}{\overbrace{r\sin \varphi} } \right )^{2} \right ]\cdot \overset{J}{\overbrace{{\color{Red} r}}}\, dr\, d\varphi =$

$\dpi{120} =\int_{0}^{2\pi }\int_{0}^{1}\left ( r^{2}\cos ^{2} \varphi +r^{2}\sin ^{2}\varphi \right )\cdot r\, dr\, d\varphi =$

Wyłączamy $\dpi{120} r^{2}$ przed nawias:

$\dpi{120} =\int_{1}^{2\pi }\int_{0}^{1}r^{2}\left (\overset{=1}{\overbrace{ \cos ^{2}\varphi +\sin ^{2}\varphi }}\right )\cdot r\, dr\, d\varphi =$

$\dpi{120} =\int_{0}^{2\pi }\left (\int_{0}^{1}r^{3}\, dr\, \right )d\varphi =$

Liczymy najpierw całkę po zmiennej $\dpi{120} r$ :

$\dpi{120} =\int_{0}^{2\pi }\left [\frac{ r^{4}}{4} \right ]_{0}^{1}d\varphi =\int_{0}^{2\pi }\left ( \frac{1^{4}}{4}-\frac{0^{4}}{4} \right )d\varphi =$

$\dpi{120} =\int_{0}^{2\pi }\frac{1}{4}\, d\varphi =\frac{1}{4}\cdot \left [ \varphi \right ]_{0}^{2\pi }=\frac{1}{4}\cdot \left (2\pi -0 \right )=\frac{1}{2}\pi$

Pokaż rozwiązanie

Zwiń

2) $\dpi{120} \underset{D\; \; \; \; }{\iint_{\, }^{\, }}e^{x^{2}+y^{2}}d\sigma ,\; \; D:\left \{ x^{2}+y^{2} \leqslant 4,\: y\leqslant 0\right \}$ ,

Rozwiązanie

Rysujemy obszar całkowania:

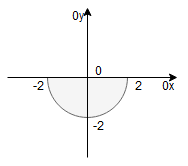
Jest to półkole o środku $\dpi{120} \left ( 0,0 \right )$ i promieniu $\dpi{120} r=2$ .

Wprowadzamy zatem współrzędne biegunowe:

$\dpi{120} x=r\cos \varphi$

$\dpi{120} y=r\sin \varphi$

Pamiętajmy o jakobianie, czyli dla współrzędnych biegunowych: $\dpi{120} {\color{Red} J=r}$ .

Ponieważ naszym obszarem całkowania jest półkole, więc zakres zmienności $\dpi{120} r$ oraz $\dpi{120} \varphi$ jest następujący:

$\dpi{120} 0\leqslant r\leqslant 2$ – długość promienia

$\dpi{120} \pi \leqslant \varphi \leqslant 2\pi$ – od ujemnej osi $\dpi{120} 0x$ czyli $\dpi{120} \pi$ , do dodatniej osi $\dpi{120} 0x$ czyli $\dpi{120} 2\pi$

$\dpi{120} \underset{D\; \; \; \; }{\iint_{\, }^{\, }}e^{x^{2}+y^{2}}d\sigma =\int_{\pi }^{2\pi }\int_{0}^{2}e^{\left ( r\cos \varphi \right )^{2}+\left ( r\sin \varphi \right )^{2}}\cdot {\color{Red} r}\, dr\, d\varphi =$

$\dpi{120} =\int_{\pi }^{2\pi }\int_{0}^{2}e^{r^{2}\cos ^{2}\varphi +r^{2}\sin ^{2}\varphi }\cdot r\, dr\, d\varphi =$

$\dpi{120} =\int_{\pi }^{2\pi }\int_{0}^{2}e^{r^{2}\left ( \cos ^{2}\varphi +\sin ^{2}\varphi \right )}\cdot r\, dr\, d\varphi =$

$\dpi{120} =\int_{\pi }^{2\pi }\left (\int_{0}^{2}e^{r^{2}}\cdot r\, dr \right )d\varphi =$

Można zapamiętać, że zawsze po wprowadzeniu współrzędnych biegunowych mamy $\dpi{120} x^{2}+y^{2}=r^{2}$ . Otrzymaliśmy całkę, którą liczymy przez podstawienie (liczymy całkę nieoznaczoną, aby nie zmieniać granic całkowania):

$\dpi{120} \int e^{r^{2}}\cdot rdr=\begin{Bmatrix} r^{2}=t\\ 2rdr=dt\\ dr=\frac{dt}{2r} \end{Bmatrix}=\int e^{t}\cdot r\cdot \frac{dt}{2r}=$

$\dpi{120} =\frac{1}{2}\int e^{t}dt=\frac{1}{2}e^{t}\overset{t=r^{2}}{=}\frac{1}{2}e^{r^{2}}$

Wracamy do naszej całki:

$\dpi{120} =\int_{\pi }^{2\pi }\frac{1}{2}\left [ e^{r^{2}} \right ]_{0}^{2}d\varphi =$

$\dpi{120} =\frac{1}{2}\int_{\pi }^{2\pi }\left ( e^{2^{2}} -e^{0^{2}}\right )d\varphi =$

$\dpi{120} =\frac{1}{2}\int_{\pi }^{2\pi }\left ( e^{4}-1 \right )d\varphi =$

Ponieważ $\dpi{120} e^{4}-1$ jest stałą, możemy czynnik ten wyłączyć przed całkę i pozostaję nam całka z jedynki. Zapamiętajmy, że taka całka jest równa długości przedziału całkowania, czyli w naszym przypadku $\dpi{120} 2\pi -\pi =\pi$ . Policzmy tą całkę również tradycyjnie:

$\dpi{120} =\frac{1}{2}\cdot \left ( e^{4}-1 \right )\int_{\pi }^{2\pi }1\, d\varphi =$

$\dpi{120} =\frac{1}{2}\cdot \left ( e^{4}-1 \right )\cdot \left [ \varphi \right ]_{\pi }^{2\pi }=$

$\dpi{120} =\frac{1}{2}\cdot \left ( e^{4}-1 \right )\cdot \left ( 2\pi -\pi \right )=$

$\dpi{120} =\frac{1}{2}\cdot \left ( e^{4}-1 \right )\cdot \pi$

Pokaż rozwiązanie

Zwiń

3) $\dpi{120} \underset{D\; \; \; \; }{\iint_{\, }^{\, }}e^{\sqrt{x^{2}+y^{2}}}d\sigma ,\; \; D:\left \{ x^{2}+y^{2} \leqslant 1,\: x\leqslant 0\right \}$ ,

Rozwiązanie

Rysujemy obszar całkowania:

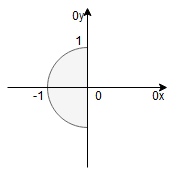
Jest to półkole o środku $\dpi{120} \left ( 0,0 \right )$ i promieniu $\dpi{120} r=1$ .

Wprowadzamy zatem współrzędne biegunowe:

$\dpi{120} x=r\cos \varphi$

$\dpi{120} y=r\sin \varphi$

Pamiętajmy o jakobianie, czyli dla współrzędnych biegunowych: $\dpi{120} {\color{Red} J=r}$ .

Ponieważ naszym obszarem całkowania jest półkole, więc zakres zmienności $\dpi{120} r$ oraz $\dpi{120} \varphi$ jest następujący:

$\dpi{120} 0\leqslant r\leqslant 1$ – długość promienia

$\dpi{120} \frac{\pi}{2} \leqslant \varphi \leqslant \frac{3}{2}\pi$ – od dodatniej osi $\dpi{120} 0y$ czyli $\dpi{120} \frac{\pi}{2}$ , do ujemnej osi $\dpi{120} 0y$ czyli $\dpi{120} \frac{3}{2}\pi$

$\dpi{120} \underset{D\; \; \; \; }{\iint_{\, }^{\, }}e^{\sqrt{x^{2}+y^{2}}}d\sigma =\int_{\frac{\pi }{2}}^{\frac{3}{2}\pi }\int_{0}^{1}e^{\sqrt{\left ( r\cos \varphi \right )^{2}+\left ( r\sin \varphi \right )^{2}}}\cdot {\color{Red} r}\, dr\, d\varphi =$

$\dpi{120} =\int_{\frac{\pi }{2}}^{\frac{3}{2}\pi }\int_{0}^{1}e^{\sqrt{r^{2}\cos ^{2}\varphi +r^{2}\sin ^{2}\varphi }}\cdot r\, dr\, d\varphi =$

$\dpi{120} =\int_{\frac{\pi }{2}}^{\frac{3}{2}\pi }\int_{0}^{1}e^{\sqrt{r^{2}\left ( \cos ^{2}\varphi +\sin ^{2}\varphi \right )}}\cdot r\, dr\, d\varphi =$

$\dpi{120} =\int_{\frac{\pi }{2}}^{\frac{3}{2}\pi }\int_{0}^{1}e^{\sqrt{r^{2}}}\cdot r\, dr\, d\varphi =$

$\dpi{120} =\int_{\frac{\pi }{2}}^{\frac{3}{2}\pi }\int_{0}^{1}e^{r}\cdot r\, dr\, d\varphi =$

Pamiętajmy, że zawsze po wprowadzeniu współrzędnych biegunowych mamy $\dpi{120} x^{2}+y^{2}=r^{2}$ . Otrzymaliśmy całkę, którą liczymy przez części (liczymy całkę nieoznaczoną, aby nie musieć pamiętać o granicach całkowania):

$\dpi{120} \int e^{r}\cdot r\, dr=\begin{Bmatrix} f=r &g'=e^{r} \\ f'=1 & g=e^{r} \end{Bmatrix}=$

$\dpi{120} =r\cdot e^{r}-\int 1\cdot e^{r}\, dr=$

$\dpi{120} =r\cdot e^{r}-e^{r}$

Wracamy do naszej całki:

$\dpi{120} =\int_{\frac{\pi }{2}}^{\frac{3}{2}\pi }\left [ re^{r} -e^{r}\right ]_{0}^{1} d\varphi =$

$\dpi{120} =\int_{\frac{\pi }{2}}^{\frac{3}{2}\pi }\left ( 1\cdot e^{1}-e^{1} -0\cdot e^{0}+e^{0}\right )d\varphi =$

$\dpi{120} =\int_{\frac{\pi }{2}}^{\frac{3}{2}\pi }1\, d\varphi =$

Pamiętamy z poprzedniego przykładu, że całka oznaczona z jedności jest równa długości przedziału całkowania. Można oczywiście liczyć tradycyjnie.

$\dpi{120} = \frac{3}{2} \pi -\frac{\pi }{2}=\pi$

Pokaż rozwiązanie

Zwiń

4) $\dpi{120} \underset{D\; \; \; \; }{\iint_{\, }^{\, }}\ln \left (1+ x^{2}+y^{2} \right )d\sigma ,\; \; D:\left \{ x^{2}+y^{2} \leqslant 1,\: \left | y \right |<x\right \}$ ,

Rozwiązanie

Rysujemy obszar całkowania:

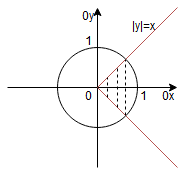
Wprowadzamy współrzędne biegunowe:

$\dpi{120} x=r\cos \varphi$

$\dpi{120} y=r\sin \varphi$

Pamiętajmy o jakobianie, czyli dla współrzędnych biegunowych: $\dpi{120} {\color{Red} J=r}$ .

Ponieważ naszym obszarem całkowania jest wycinek koła, więc zakres zmienności $\dpi{120} r$ oraz $\dpi{120} \varphi$ jest następujący:

$\dpi{120} 0\leqslant r\leqslant 1$ – długość promienia

$\dpi{120} -\frac{\pi}{4} \leqslant \varphi \leqslant\frac{\pi}{4}$ – proste $\dpi{120} y=-x$ i $\dpi{120} y=x$ tworzą z dodatnimi półosiami $\dpi{120} 0x$ kąt $\dpi{120} \frac{\pi }{4}$ .

$\dpi{120} \underset{D\; \; \; \; }{\iint_{\, }^{\, }}\ln \left (1+ x^{2}+y^{2} \right )d\sigma =\int_{-\frac{\pi }{4}}^{\frac{\pi }{4}}\int_{0}^{1}\ln \left [ 1+\overset{=r^{2}}{\overbrace{\left ( r\cos \varphi \right )^{2} +\left ( r\sin \varphi \right )^{2}}}\right ]\cdot {\color{Red} r}\, dr\, d\phi =$

Z poprzednich przykładów już pamiętamy, że zawsze po wprowadzeniu współrzędnych biegunowych mamy $\dpi{120} x^{2}+y^{2}=r^{2}$ . Zatem:

$\dpi{120} =\int_{-\frac{\pi }{4}}^{\frac{\pi }{4}}\int_{0}^{1}r\cdot \ln \left ( 1+r^{2} \right )dr\, d\varphi =$

Liczymy tę całkę przez podstawienie, ale najpierw jako całkę nieoznaczoną:

$\dpi{120} \int r\cdot \ln \left ( 1+r^{2} \right )dr=\begin{Bmatrix} 1+r^{2}=t\\ 2rdr=dt\\ dr=\frac{dt}{2r} \end{Bmatrix}=\int r\cdot \ln t\cdot \frac{dt}{2r}=$

$\dpi{120} =\frac{1}{2}\int \ln t\, dt=$

Wykorzystujemy wzór, bądź liczymy tę całkę przez części (jest w temacie całkowanie przez części):

$\dpi{120} \int \ln x\, dx=x \ln x-x$

Mamy:

$\dpi{120} =\frac{1}{2}\int \ln t\, dt=\frac{1}{2}\cdot \left ( t\ln t-t \right )\overset{t=1+r^{2}}{=}\frac{1}{2}\cdot \left [ \left ( 1+r^{2} \right ) \ln \left ( 1+r^{2} \right ) -\left ( 1+r^{2} \right )\right ]$

Wracamy do całki podwójnej:

$\dpi{120} =\int_{-\frac{\pi }{4}}^{\frac{\pi }{4}}\int_{0}^{1}r\cdot \ln \left ( 1+r^{2} \right )dr\, d\varphi =$

$\dpi{120} =\frac{1}{2}\int_{-\frac{\pi }{4}}^{\frac{\pi }{4}} \left [ \left ( 1+r^{2} \right ) \ln \left ( 1+r^{2} \right ) -\left ( 1+r^{2} \right )\right ]_{0}^{1}d\varphi =$

$\dpi{120} =\frac{1}{2}\int_{-\frac{\pi }{4}}^{\frac{\pi }{4}} \left [ \left ( 1+1^{2} \right ) \ln \left ( 1+1^{2} \right ) -\left ( 1+1^{2} \right )-\left ( 1+0^{2} \right ) \overset{=0}{\overbrace{\ln \left ( 1+0^{2} \right )} }+\left ( 1+0^{2} \right )\right ]d\varphi =$

$\dpi{120} =\frac{1}{2}\int_{-\frac{\pi }{4}}^{\frac{\pi }{4}}\left ( 2\ln 2-2+1 \right )d\varphi =$

$\dpi{120} =\frac{1}{2}\int_{-\frac{\pi }{4}}^{\frac{\pi }{4}}\left ( 2\ln 2-1 \right )d\varphi =$

$\dpi{120} 2\ln 2-1$ jest stałą, więc można ją wyłączyć przed całkę, a więc mamy całkę z jedynki, a to na podstawie wcześniejszych przykładów jest równe długości przedziału całkowania. Mamy:

$\dpi{120} =\frac{1}{2}\cdot \left ( 2\ln 2-1 \right )\cdot \left ( \frac{\pi }{4} -\left ( -\frac{\pi }{4} \right )\right )=$

$\dpi{120} =\frac{1}{2}\cdot \left ( 2\ln 2-1 \right )\cdot \frac{\pi }{2}=\frac{\pi }{4}\cdot \left ( 2\ln 2-1 \right )$

Pokaż rozwiązanie

Zwiń

5) $\dpi{120} \underset{D\; \; \; \; }{\iint_{\, }^{\, }}\frac{1-x^{2}-y^{2}}{1+x^{2}+y^{2}}\, d\sigma ,\; \; D:\left \{ 1\leqslant x^{2}+y^{2} \leqslant 4\right \}$ ,

Rozwiązanie

Rysujemy obszar całkowania:

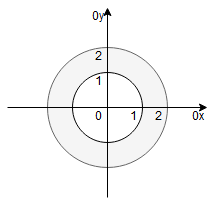
Wprowadzamy współrzędne biegunowe:

$\dpi{120} x=r\cos \varphi$

$\dpi{120} y=r\sin \varphi$

Pamiętajmy o jakobianie, czyli dla współrzędnych biegunowych: $\dpi{120} {\color{Red} J=r}$ .

Ponieważ naszym obszarem całkowania jest pierścień, więc zakres zmienności $\dpi{120} r$ oraz $\dpi{120} \varphi$ jest następujący:

$\dpi{120} 1\leqslant r\leqslant 2$ – długość promienia

$\dpi{120} 0 \leqslant \varphi \leqslant2\pi$ – mamy cały pierścień

$\dpi{120} \underset{D\; \; \; \; }{\iint_{\, }^{\, }}\frac{1-x^{2}-y^{2}}{1+x^{2}+y^{2}}\, d\sigma =\underset{D\; \; \; \; }{\iint_{\, }^{\, }}\frac{1-\left (x^{2}+y^{2} \right )}{1+x^{2}+y^{2}}\, d\sigma =$

$\dpi{120} =\int_{0}^{2\pi }\int_{1}^{2}\frac{1-\overset{=r^{2}}{\overbrace{\left [ \left ( r\cos \varphi \right )^{2} +\left ( r\sin \varphi \right )^{2}\right ]}}}{1+\underset{=r^{2}}{\underbrace{\left ( r\cos \varphi \right )^{2}+\left ( r\sin \varphi \right )^{2}}}} \cdot {\color{Red} r}\, dr\, d\varphi =$

Z poprzednich przykładów już pamiętamy, że zawsze po wprowadzeniu współrzędnych biegunowych mamy $\dpi{120} x^{2}+y^{2}=r^{2}$ . Zatem:

$\dpi{120} =\int_{0}^{2\pi }\int_{1}^{2}\frac{1-r^{2}}{1+r^{2}}\cdot r\, dr\, d\varphi =$

Liczymy całkę $\dpi{120} \int \frac{1-r^{2}}{1+r^{2}}\cdot r\, dr$ przez podstawienie:

$\dpi{120} \int \frac{1-r^{2}}{1+r^{2}}\cdot r\, dr=\begin{Bmatrix} 1+r^{2}=t\\ 2rdr=dt\\ dr=\frac{dt}{2r} \end{Bmatrix}=$

$\dpi{120} =\int \frac{1-\left ( t-1 \right )}{t}\cdot r\cdot \frac{dt}{2r}=$

$\dpi{120} =\frac{1}{2}\int \frac{2-t}{t}\, dt=\frac{1}{2}\int \left ( \frac{2}{t} -1\right )dt=$

$\dpi{120} =\frac{1}{2}\cdot \left ( 2\ln t -t\right )\overset{t=1+r^{2}}{=}\frac{1}{2}\left [ 2\ln \left ( 1+r^{2} \right ) -\left ( 1+r^{2} \right )\right ]$

Wracamy do całki podwójnej:

$\dpi{120} =\int_{0}^{2\pi }\int_{1}^{2}\frac{1-r^{2}}{1+r^{2}}\cdot r\, dr\, d\varphi =$

$\dpi{120} =\frac{1}{2}\int_{0}^{2\pi }\left [ 2\ln \left ( 1+r^{2} \right )-\left ( 1+r^{2} \right )\right ]_{1}^{2}d\varphi =$

$\dpi{120} =\frac{1}{2}\int_{0}^{2\pi }\left [ 2\ln \left ( 1+2^{2} \right )-\left ( 1+2^{2} \right )-2\ln \left ( 1+1^{2} \right )+\left ( 1+1^{2} \right )\right ]d\varphi =$

$\dpi{120} =\frac{1}{2}\int_{0}^{2\pi }\left [ 2\ln 5-5-2 \ln 2+2 \right ]d\varphi =$

Wykorzystujemy własność logarytmów $\dpi{120} \ln x- \ln y= \ln \frac{x}{y}$ :

$\dpi{120} =\frac{1}{2}\int_{0}^{2\pi }\left [ 2\ln \frac{5}{2}-3\right ]d\varphi =$

Stałą $\dpi{120} 2\ln \frac{5}{2}-3$ wyłączamy przed całkę i podobnie jak w poprzednich przykładach otrzymujemy całkę z jedynki, która jest równa długości przedziału całkowania czyli $\dpi{120} 2\pi$ :

$\dpi{120} =\frac{1}{2}\cdot \left ( 2\ln \frac{5}{2}-3\right )\cdot 2\pi =\pi \cdot \left ( 2\ln \frac{5}{2}-3\right )$

Pokaż rozwiązanie

Zwiń

6) $\dpi{120} \underset{D\; \; \; \; }{\iint_{\, }^{\, }}xy\, d\sigma ,\; \; D:\left \{ x^{2}+y^{2} \leqslant 9,\: x\leqslant 0,\: y\leqslant 0\right \}$ ,

Rozwiązanie

Rysujemy obszar całkowania:

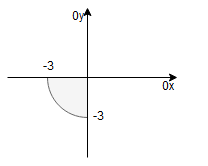
Wprowadzamy współrzędne biegunowe:

$\dpi{120} x=r\cos \varphi$

$\dpi{120} y=r\sin \varphi$

Pamiętajmy o jakobianie, czyli dla współrzędnych biegunowych: $\dpi{120} {\color{Red} J=r}$ .

Ponieważ naszym obszarem całkowania jest ćwiartka koła, więc zakres zmienności $\dpi{120} r$ oraz $\dpi{120} \varphi$ jest następujący:

$\dpi{120} 0\leqslant r\leqslant 3$ – długość promienia, częsty błąd – studenci podają: $\dpi{120} -3\leqslant r\leqslant 0$ . Pamiętajmy $\dpi{120} r$ jest długością promienia.

$\dpi{120} \pi \leqslant \varphi \leqslant\frac{3}{2}\pi$ – III ćwiartka układu współrzędnych

$\dpi{120} \underset{D\; \; \; \; }{\iint_{\, }^{\, }}xy\, d\sigma =\int_{\pi }^{\frac{3}{2}\pi }\int_{0}^{3}\left ( r\cos \varphi \right )\cdot \left ( r\sin \varphi \right )\cdot {\color{Red} r}\, dr \, d\varphi =$

$\dpi{120} =\int_{\pi }^{\frac{3}{2}\pi }\int_{0}^{3} r^{3}\cdot \overset{=\frac{1}{2}\sin 2\varphi }{\overbrace{\cos \varphi \cdot \sin \varphi }}\, dr \, d\varphi =$

Wykorzystaliśmy wzór $\dpi{120} \sin 2\alpha =2 \sin \alpha \cos \alpha.$ Stałą $\dpi{120} \frac{1}{2}$ wyłączamy przed całki, zaś $\dpi{120} \sin 2\varphi$ przed jedną z całek, gdyż nie zależy od zmiennej $\dpi{120} r$ .

$\dpi{120} =\frac{1}{2}\int_{\pi }^{\frac{3}{2}\pi }\sin 2\varphi \left (\int_{0}^{3} r^{3}\, dr \right )\, d\varphi =$

$\dpi{120} =\frac{1}{2}\int_{\pi }^{\frac{3}{2}\pi }\sin 2\varphi\cdot \left [ \frac{r^{4}}{4} \right ]_{0}^{3}\, d\varphi =$

$\dpi{120} =\frac{1}{2}\int_{\pi }^{\frac{3}{2}\pi }\sin 2\varphi\cdot \overset{\frac{81}{4}}{\overbrace{\left ( \frac{3^{4}}{4} -\frac{0^{4}}{4}\right )}}\, d\varphi =$

$\dpi{120} =\frac{1}{2}\cdot \frac{81}{4}\int_{\pi }^{\frac{3}{2}\pi }\sin 2\varphi\, d\varphi =$

Wykorzystujemy wzór:

$\dpi{120} \int \sin \left ( ax+b \right )dx=-\frac{1}{a}\cos \left ( ax+b \right )$

$\dpi{120} =\frac{81}{8}\cdot \left [ -\frac{1}{2} \cos 2\varphi \right ]_{\pi }^{\frac{3}{2}\pi }=$

$\dpi{120} =-\frac{81}{16}\left ( \cos 2\cdot \frac{3}{2}\pi - \cos 2\pi \right )=$

$\dpi{120} =-\frac{81}{16}\left ( \cos 3\pi - \cos 2\pi \right )=$

$\dpi{120} =-\frac{81}{16}\left ( \overset{-1}{\overbrace{\cos \pi}} - \overset{1}{\overbrace{\cos 2\pi}} \right )=-\frac{81}{16}\cdot \left ( -2 \right )=\frac{81}{8}$

Pokaż rozwiązanie

Zwiń

7) $\dpi{120} \underset{D\; \; \; \; }{\iint_{\, }^{\, }}arc\, tg\, \frac{y}{x}\, d\sigma ,\; \; D:\left \{ 1\leqslant x^{2}+y^{2} \leqslant 4,\: x\leqslant 0,\: y\geqslant 0\right \}$ .

Rozwiązanie

Rysujemy obszar całkowania:

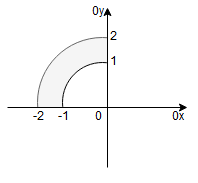
Wprowadzamy współrzędne biegunowe:

$\dpi{120} x=r\cos \varphi$

$\dpi{120} y=r\sin \varphi$

Pamiętajmy o jakobianie, czyli dla współrzędnych biegunowych: $\dpi{120} {\color{Red} J=r}$ .

Ponieważ naszym obszarem całkowania jest ćwiartka pierścienia, więc zakres zmienności $\dpi{120} r$ oraz $\dpi{120} \varphi$ jest następujący:

$\dpi{120} 1\leqslant r\leqslant 2$ – długość promienia, częsty błąd – studenci podają: $\dpi{120} -2\leqslant r\leqslant -1$ . Pamiętajmy $\dpi{120} r$ jest długością promienia.

$\dpi{120} \frac{\pi}{2} \leqslant \varphi \leqslant\pi$ – II ćwiartka układu współrzędnych

$\dpi{120} \underset{D\; \; \; \; }{\iint_{\, }^{\, }}arc\, tg\, \frac{y}{x}\, d\sigma =\int_{\frac{\pi }{2}}^{\pi }\int_{1}^{2}arc\, tg\, \frac{r\sin \varphi }{r\cos \varphi }\cdot {\color{Red} r}\, dr\, d\varphi =$

$\dpi{120} =\int_{\frac{\pi }{2}}^{\pi }\int_{1}^{2}r\cdot arc\, tg\, \overset{=tg\, \varphi }{\overbrace{\frac{\sin \varphi }{\cos \varphi }}}\, dr\, d\varphi =$

$\dpi{120} =\int_{\frac{\pi }{2}}^{\pi }\int_{1}^{2}r\cdot \overset{=\varphi }{\overbrace{arc\, tg\, \left (tg\varphi \right ) }}\, dr\, d\varphi =$

Pamiętajmy, że funkcja arcus tangens jest funkcją odwrotną do funkcji tangens, stąd redukcja do $\dpi{120} \varphi$ .

$\dpi{120} =\int_{\frac{\pi }{2}}^{\pi }\int_{1}^{2}r\cdot \varphi \, dr\, d\varphi =$

$\dpi{120} =\int_{\frac{\pi }{2}}^{\pi }\varphi \int_{1}^{2}r\, dr\, d\varphi =$

$\dpi{120} =\int_{\frac{\pi }{2}}^{\pi }\varphi \cdot \left [ \frac{r^{2}}{2} \right ]_{1}^{2}\, d\varphi =$

$\dpi{120} =\int_{\frac{\pi }{2}}^{\pi }\varphi \cdot \overset{=\frac{3}{2}}{\overbrace{\left [ \frac{2^{2}}{2}-\frac{1^{2}}{2} \right ]}}\, d\varphi =$

$\dpi{120} =\frac{3}{2}\int_{\frac{\pi }{2}}^{\pi }\varphi \, d\varphi =\frac{3}{2}\cdot \left [ \frac{\varphi ^{2}}{2} \right ]_{\frac{\pi }{2}}^{\pi }=$

$\dpi{120} =\frac{3}{2}\cdot \left ( \frac{\pi ^{2}}{2}-\frac{\left ( \frac{\pi }{2} \right )^{2}}{2} \right )=\frac{3}{2}\cdot \frac{3}{8}\pi ^{2}=\frac{9}{16}\pi ^{2}$

Pokaż rozwiązanie

Zwiń

Zadanie 2. Obliczyć objętość figury

$\dpi{120} \large F=\left \{ \left ( x,y,z \right ):\left ( x,y \right ) \in D,\: 0\leqslant z\leqslant z\left ( x,y \right )\right \}$ :

Korzystamy ze wzoru na objętość figury $\dpi{120} F$ :

$\dpi{120} V_{F}=\underset{D\; \; \; \; }{\iint_{\, }^{\, }}z\left ( x,y \right )d\sigma$

1) $\dpi{120} D=\left \{ \left | x \right | \leqslant 1,\: \left | y \right |\leqslant 1\right \},\; z\left ( x,y \right )=2x+3y+7$ ,

Rozwiązanie

Korzystając z powyższego wzoru, objętość figury $\dpi{120} F$ wyrazi się całką:

$\dpi{120} V_{F}=\underset{D\; \; \; \; }{\iint_{\, }^{\, }}\left (2x+3y+7 \right )d\sigma$ , gdzie $\dpi{120} D=\left \{ \left | x \right | \leqslant 1,\: \left | y \right |\leqslant 1\right \}$

Narysujmy obszar całkowania $\dpi{120} D$ :

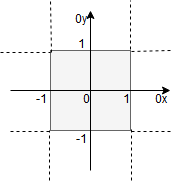
Jak widać:

$\dpi{120} -1\leqslant x\leqslant 1$

$\dpi{120} -1\leqslant y\leqslant 1$

Zatem całka podwójna zapisze się jako:

$\dpi{120} V_{F}=\underset{D\; \; \; \; }{\iint_{\, }^{\, }}\left (2x+3y+7 \right )d\sigma=\int_{-1}^{1}\int_{-1}^{1}\left ( 2x+3y+7 \right )dxdy$

Kolejność różniczek $\dpi{120} dx\, dy$ nie ma znaczenia, gdyż granice całkowania obydwu zmiennych są takie same od -1 do 1. Zatem:

$\dpi{120} V_{F}=\int_{-1}^{1}\int_{-1}^{1}\left ( 2x+3y+7 \right )dxdy=$

$\dpi{120} =\int_{-1}^{1}\left [ 2\cdot \frac{x^{2}}{2}+3yx+7x \right ]_{-1}^{1}dy=$

$\dpi{120} =\int_{-1}^{1}\left [ x^{2}+3yx+7x \right ]_{-1}^{1}dy=$

$\dpi{120} =\int_{-1}^{1}\left [ 1^{2}+3y\cdot 1+7\cdot 1 -\left ( -1 \right )^{2}-3y\cdot \left ( -1 \right )-7\cdot \left ( -1 \right )\right ]dy=$

$\dpi{120} =\int_{-1}^{1}\left ( 1+3y+7-1+3y+7 \right )dy=$

$\dpi{120} =\int_{-1}^{1}\left ( 6y+14 \right )dy=$

$\dpi{120} =\left [ 6\cdot \frac{y^{2}}{2} +14y\right ]_{-1}^{1}=$

$\dpi{120} =6\cdot \frac{1^{2}}{2} +14\cdot 1-6\cdot \frac{\left (-1 \right )^{2}}{2} -14\cdot \left (-1 \right ) =$

$\dpi{120} =3+14-3+14=28$

Liczyliśmy objętość, więc każdy wynik ujemny mówiłby o popełnionym błędzie.

Pokaż rozwiązanie

Zwiń

2) $\dpi{120} D=\left \{ x^{2}+y^{2}\leqslant 9 \right \},\; z\left ( x,y \right )=9-x-y$ .

Rozwiązanie

Korzystając ze wzoru na objętość, objętość figury $\dpi{120} F$ wyrazi się całką:

$\dpi{120} V_{F}=\underset{D\; \; \; \; }{\iint_{\, }^{\, }}\left (9-x-y\right )d\sigma$ , gdzie $\dpi{120} D=\left \{ x^{2}+y^{2}\leqslant 9 \right \}$

Narysujmy obszar całkowania $\dpi{120} D$ :

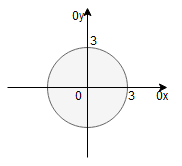
Obszar $\dpi{120} D$ jest kołem, więc wprowadzamy współrzędne biegunowe:

$\dpi{120} x=r\cos \varphi$

$\dpi{120} y=r\sin \varphi$

Pamiętajmy o jakobianie, czyli dla współrzędnych biegunowych: $\dpi{120} {\color{Red} J=r}$ .

Ponieważ naszym obszarem całkowania jest pełne koło, więc zakres zmienności $\dpi{120} r$ oraz $\dpi{120} \varphi$ jest następujący:

$\dpi{120} 0\leqslant r\leqslant 3$ – długość promienia,

$\dpi{120} 0 \leqslant \varphi \leqslant2\pi$ – pełne koło

Zatem całka podwójna zapisze się jako:

$\dpi{120} V_{F}=\underset{D\; \; \; \; }{\iint_{\, }^{\, }}\left (9-x-y\right )d\sigma=\int_{0}^{2\pi }\int_{0}^{3}\left ( 9-r\cos \varphi -r\sin \varphi \right )\cdot {\color{Red} r}\, dr\, d\varphi =$

$\dpi{120} =\int_{0}^{2\pi }\int_{0}^{3}\left ( 9r-r^{2}\cos \varphi -r^{2}\sin \varphi \right )\, dr\, d\varphi =$

$\dpi{120} =\int_{0}^{2\pi }\left [ 9\cdot \frac{r^{2}}{2}-\frac{r^{3}}{3}\cdot \cos \varphi -\frac{r^{3}}{3}\cdot \sin \varphi \right ]_{0}^{3}d\varphi =$

$\dpi{120} =\int_{0}^{2\pi }\left ( 9\cdot \frac{3^{2}}{2}-\frac{3^{3}}{3}\cdot \cos \varphi -\frac{3^{3}}{3}\cdot \sin \varphi \right )d\varphi =$

$\dpi{120} =\int_{0}^{2\pi }\left ( \frac{81}{2}-9\cos \varphi -9\sin \varphi \right )d\varphi =$

Warto zapamiętać, że $\dpi{120} \int_{0}^{2\pi }\sin x\, dx=0$ oraz $\dpi{120} \int_{0}^{2\pi }\cos x\, dx=0$ . Wynika to z okresowości tych funkcji. Jeżeli tego nie pamiętamy, to liczymy tradycyjnie. Będzie po prostu dłużej.

$\dpi{120} =\left [ \frac{81}{2} \varphi -9\sin \varphi +9\cos \varphi \right ]_{0}^{2\pi }=...$

Wykorzystując wspomniany wyżej fakt mamy:

$\dpi{120} =\frac{81}{2}\cdot \left ( 2\pi -0 \right )=81\pi$

Pokaż rozwiązanie

Zwiń

Zadanie 3. Obliczyć objętość figury ograniczonej powierzchniami:

Ponownie korzystamy ze wzoru na objętość figury $\dpi{120} F$ :

$\dpi{120} V_{F}=\underset{D\; \; \; \; }{\iint_{\, }^{\, }}z\left ( x,y \right )d\sigma$

1) $\dpi{120} x=0,\: y=2x,\: y=1,\: z=0,\: z=x^{2}+y^{2}$ ,

Rozwiązanie

Najpierw należy znaleźć obszar całkowania $\dpi{120} D$ . Jest on opisany równaniami: $\dpi{120} x=0,\: y=2x,\: y=1,\: z=0$ .

Narysujmy go.

Opiszmy ten obszar nierównościami:

$\dpi{120} 0\leqslant x\leqslant \frac{1}{2}$

$\dpi{120} 2x\leqslant y\leqslant 1$

Zatem objętość wyrazi się wzorem:

$\dpi{120} V=\underset{D\; \; \; \; }{\iint_{\, }^{\, }}z\left ( x,y \right )d\sigma=\int_{0}^{\frac{1}{2}}\int_{2x}^{1}\left ( x^{2}+y^{2} \right )dy\, dx=$

Najpierw liczymy całkę po zmiennej $\dpi{120} y$ :

$\dpi{120} =\int_{0}^{\frac{1}{2}}\left [ x^{2} y+\frac{y^{3}}{3}\right ]_{2x}^{1}dx=$

$\dpi{120} =\int_{0}^{\frac{1}{2}}\left ( x^{2} \cdot 1+\frac{1^{3}}{3}-x^{2}\cdot 2x-\frac{\left ( 2x \right )^{3}}{3}\right )dx=$

$\dpi{120} =\int_{0}^{\frac{1}{2}}\left ( x^{2}+\frac{1}{3} -2x^{3}-\frac{8}{3}x^{3}\right )dx=$

$\dpi{120} =\int_{0}^{\frac{1}{2}}\left ( -\frac{14}{3}x^{3}+x^{2}+\frac{1}{3}\right )dx=$

$\dpi{120} =\left [ -\frac{14}{3}\cdot \frac{x^{4}}{4} +\frac{x^{3}}{3}+\frac{1}{3}x\right ]_{0}^{\frac{1}{2}}=$

$\dpi{120} =-\frac{7}{6}\cdot \left ( \frac{1}{2} \right )^{4}+\frac{1}{3}\cdot \left ( \frac{1}{2} \right )^{3}+\frac{1}{3}\cdot \frac{1}{2}-0=$

$\dpi{120} =-\frac{7}{96}+\frac{1}{24}+\frac{1}{6}=\frac{13}{96}$

Objętość figury wynosi $\dpi{120} \frac{13}{96}$ .

Pokaż rozwiązanie

Zwiń

2) $\dpi{120} 2z=4-x^{2}-y^{2},\: z=0$ ,

Rozwiązanie

Najpierw należy znaleźć obszar całkowania $\dpi{120} D$ . Jest to obszar leżący w płaszczyźnie $\dpi{120} 0xy$ więc do funkcji $\dpi{120} 2z=4-x^{2}-y^{2}$ wstawiamy $\dpi{120} z=0$ . Otrzymujemy:

$\dpi{120} 0=4-x^{2}-y^{2}\Leftrightarrow x^{2}+y^{2}=4$

Jako obszar $\dpi{120} D$ otrzymaliśmy zatem koło o środku w punkcie $\dpi{120} \left ( 0,0 \right )$ i promieniu $\dpi{120} r=2$ , co przedstawia rysunek:

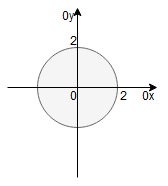
Ponieważ obszarem całkowania jest koło, wprowadzamy współrzędne biegunowe:

$\dpi{120} x=r\cos \varphi$

$\dpi{120} y=r\sin \varphi$

Pamiętajmy o jakobianie, czyli dla współrzędnych biegunowych: $\dpi{120} {\color{Red} J=r}$ .

Zakres zmienności $\dpi{120} r$ oraz $\dpi{120} \varphi$ jest następujący:

$\dpi{120} 0\leqslant r\leqslant 2$ – długość promienia,

$\dpi{120} 0 \leqslant \varphi \leqslant2\pi$ – pełne koło

Funkcję podcałkową $\dpi{120} z\left ( x,y \right )$ wyliczamy z zależności:

$\dpi{120} 2z=4-x^{2}-y^{2}/:2\Rightarrow z=2-\frac{x^{2}}{2}-\frac{y^{2}}{2}$

Objętość naszej figury zapisze się wzorem:

$\dpi{120} V=\underset{D\; \; \; \; }{\iint_{\, }^{\, }}z\left ( x,y \right )d\sigma=\underset{D\; \; \; \; }{\iint_{\, }^{\, }}\left ( 2-\frac{x^{2}}{2} -\frac{y^{2}}{2}\right )d\sigma=$

$\dpi{120} =\int_{0}^{2\pi }\int_{0}^{2}\left [ 2-\frac{1}{2}\cdot \overset{=r^{2}}{\overbrace{\left [\left ( r\cos \varphi \right )^{2} +\left ( r\sin \varphi \right )^{2} \right ]}}\right ]\cdot {\color{Red} r}\, dr\, d\varphi =$

$\dpi{120} =\int_{0}^{2\pi }\int_{0}^{2}\left [ 2-\frac{1}{2}\cdot r^{2}\right ]\cdot r\, dr\, d\varphi =$

$\dpi{120} =\int_{0}^{2\pi }\int_{0}^{2}\left ( 2r-\frac{1}{2} r^{3}\right )dr\, d\varphi =$

$\dpi{120} =\int_{0}^{2\pi }\left [ 2\cdot \frac{r^{2}}{2} -\frac{1}{2}\cdot \frac{r^{4}}{4}\right ]_{0}^{2}d\varphi =$

$\dpi{120} =\int_{0}^{2\pi }\left [ r^{2}-\frac{1}{8}r^{4} \right ]_{0}^{2}d\varphi =$

$\dpi{120} =\int_{0}^{2\pi }\left ( 2^{2}-\frac{1}{8} \cdot 2^{4}-0\right )d\varphi =\int_{0}^{2\pi }\left ( 4-2 \right )d\varphi =$

$\dpi{120} =2\int_{0}^{2\pi }1\, d\varphi =2\cdot \left ( 2\pi -0 \right )=4\pi$

Objętość figury wynosi $\dpi{120} 4\pi$ .

Pokaż rozwiązanie

Zwiń

3) $\dpi{120} 4z=16-x^{2}-y^{2},\: z=0,\: x^{2}+y^{2}=4$ .

Rozwiązanie

Najpierw należy znaleźć obszar całkowania $\dpi{120} D$ . Jest to obszar leżący w płaszczyźnie $\dpi{120} 0xy$ więc do funkcji $\dpi{120} 4z=16-x^{2}-y^{2}$ wstawiamy $\dpi{120} z=0$ . Otrzymujemy:

$\dpi{120} 0=16-x^{2}-y^{2}\Leftrightarrow x^{2}+y^{2}=16$

Ale w zadaniu mieliśmy jeszcze w płaszczyźnie $\dpi{120} 0xy$ koło $\dpi{120} x^{2}+y^{2}=4$ . Zatem obszarem $\dpi{120} D$ jest część wspólna tych dwu obszarów. Przedstawia to rysunek:

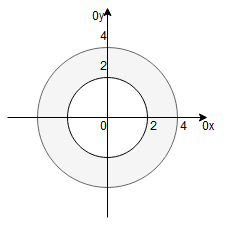
Ponieważ obszarem całkowania jest pierścień, wprowadzamy współrzędne biegunowe:

$\dpi{120} x=r\cos \varphi$

$\dpi{120} y=r\sin \varphi$

Pamiętajmy o jakobianie, czyli dla współrzędnych biegunowych: $\dpi{120} {\color{Red} J=r}$ .

Zakres zmienności $\dpi{120} r$ oraz $\dpi{120} \varphi$ jest następujący:

$\dpi{120} 2\leqslant r\leqslant 4$ – długość promienia,

$\dpi{120} 0 \leqslant \varphi \leqslant2\pi$ – cały pierścień

Funkcję podcałkową $\dpi{120} z\left ( x,y \right )$ wyliczamy z zależności:

$\dpi{120} 4z=16-x^{2}-y^{2}/:4\Rightarrow z=4-\frac{x^{2}}{4}-\frac{y^{2}}{4}$

Objętość naszej figury zapisze się wzorem:

$\dpi{120} V=\underset{D\; \; \; \; }{\iint_{\, }^{\, }}z\left ( x,y \right )d\sigma=\underset{D\; \; \; \; }{\iint_{\, }^{\, }}\left ( 4-\frac{x^{2}}{4} -\frac{y^{2}}{4}\right )d\sigma=$

$\dpi{120} =\int_{0}^{2\pi }\int_{2}^{4}\left [ 4-\frac{1}{4} \cdot \overset{=r^{2}}{\overbrace{\left [ \left ( r\cos \varphi \right )^{2} +\left ( r\sin \varphi \right )^{2}\right ]}}\right ]\cdot {\color{Red} r}\, dr\, d\varphi =$

$\dpi{120} =\int_{0}^{2\pi }\int_{2}^{4}\left [ 4-\frac{1}{4}\cdot r^{2}\right ]\cdot r\, dr\, d\varphi =$

$\dpi{120} =\int_{0}^{2\pi }\int_{2}^{4}\left ( 4r-\frac{1}{4} r^{3}\right )dr\, d\varphi =$

$\dpi{120} =\int_{0}^{2\pi }\left [ 4\cdot \frac{r^{2}}{2} -\frac{1}{4}\cdot \frac{r^{4}}{4}\right ]_{2}^{4}d\varphi =$

$\dpi{120} =\int_{0}^{2\pi }\left [ 2r^{2}-\frac{1}{16}r^{4} \right ]_{2}^{4}d\varphi =$

$\dpi{120} =\int_{0}^{2\pi }\left (2\cdot 4^{2}-\frac{1}{16} \cdot 4^{4}-2\cdot 2^{2}+\frac{1}{16}\cdot 2^{4}\right )d\varphi =$

$\dpi{120} =\int_{0}^{2\pi }\left (32-16-8+ 1\right )d\varphi =$

$\dpi{120} =9\int_{0}^{2\pi }1\, d\varphi =9\cdot \left ( 2\pi -0 \right )=18\pi$

Objętość figury wynosi $\dpi{120} 18\pi$ .

Pokaż rozwiązanie

Zwiń