Przed rozpoczęciem zadań warto zajrzeć do zakładki Teoria tutaj, gdzie podajemy definicję iloczynu kartezjańskiego.
Zadanie 1. Znaleźć iloczyn kartezjański i
zbiorów:
1)
Rozwiązanie Rozwiązanie przedstawimy w układzie współrzędnych. Na osi Na osi 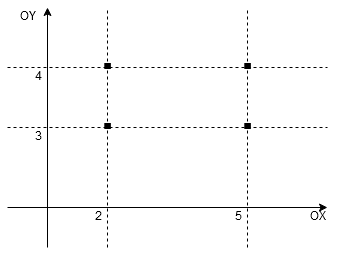
zaznaczamy zbiór
, zaś na osi
zbiór
. Jako
otrzymujemy cztery punkty o współrzędnych
.
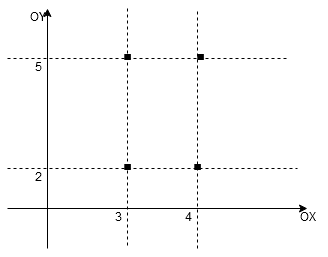
zaznaczamy zbiór
, zaś na osi
zbiór
. Jako
otrzymujemy cztery punkty o współrzędnych
.
2)
Rozwiązanie Rozwiązanie przedstawimy w układzie współrzędnych. Na osi Na osi Uważajmy, gdzie przedziały były domknięte a gdzie otwarte. Zaznaczamy odpowiednio linie ciągłe i przerywane.
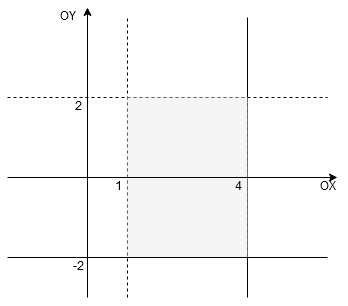
zaznaczamy zbiór
, zaś na osi
zbiór
. Jako
otrzymujemy prostokąt zacieniowany na szaro.
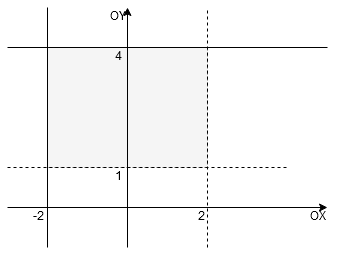
zaznaczamy zbiór
, zaś na osi
zbiór
. Jako
otrzymujemy prostokąt zacieniowany na szaro.
3)
Rozwiązanie Rozwiązanie przedstawimy w układzie współrzędnych. Na osi Na osi Uważajmy, gdzie przedziały były domknięte a gdzie otwarte. Zaznaczamy odpowiednio linie ciągłe i przerywane.

zaznaczamy zbiór
, zaś na osi
zbiór
. Jako
otrzymujemy prostokąt zacieniowany na szaro.
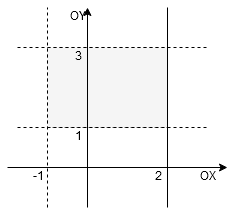
zaznaczamy zbiór
, zaś na osi
zbiór
. Jako
otrzymujemy prostokąt zacieniowany na szaro.
4)
Rozwiązanie Rozwiązanie przedstawimy w układzie współrzędnych. Na osi Na osi Uważajmy, gdzie przedziały były domknięte a gdzie otwarte. Zaznaczamy odpowiednio linie ciągłe i przerywane.
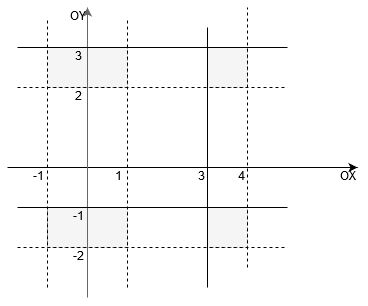
zaznaczamy zbiór
, zaś na osi
zbiór
. Jako
otrzymujemy cztery prostokąty zacieniowane na szaro.
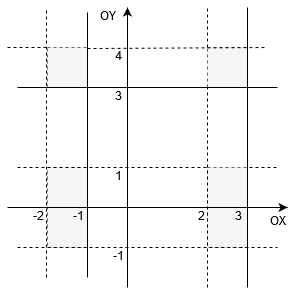
zaznaczamy zbiór
, zaś na osi
zbiór
. Jako
otrzymujemy cztery prostokąty zacieniowane na szaro.
Zadanie 2. Sprawdzić, czy prawdziwe są równości:
1)
Rozwiązanie
Niech element należy do lewej strony. Mamy:
Z definicji iloczynu kartezjańskiego otrzymujemy:
Z definicji sumy zbiorów mamy:
Stosujemy prawo rozdzielności koniunkcji względem alternatywy:
Co należało pokazać.
2)
Rozwiązanie Niech element Z definicji iloczynu kartezjańskiego otrzymujemy: Z definicji sumy zbiorów mamy: Stosujemy prawo łączności koniunkcji: Wyrażenie Co należało pokazać. należy do lewej strony. Mamy:
możemy powtórzyć jeszcze raz.
3)
Rozwiązanie Niech w tym przykładzie element Z definicji różnicy zbiorów otrzymujemy: Z definicji iloczynu kartezjańskiego mamy: Stosujemy prawo de Morgana: Stosujemy prawo przemienności i łączności koniunkcji: Stosujemy prawo rozdzielności koniunkcji względem alternatywy: Zauważmy, że wyrażenie Ponownie stosujemy prawo przemienności i łączności koniunkcji: Co należało pokazać. należy do prawej strony (łatwiej). Mamy:
jest zawsze fałszywe. Zatem alternatywa w nawiasie kwadratowym zależy tylko od drugiego składnika. Mamy: