Całki potrójne (zadania) - WYZNACZNIK

Zadanie 1. Obliczyć całki potrójne po prostopadłościanie:

1) $\dpi{120} \underset{D\; \; \; \: }{\iiint_{\, }^{\, }}\left ( x+y+z \right )d\sigma ,\; \: D=\left \{ 0\leqslant x\leqslant 1,\: 0\leqslant y\leqslant 2,\: 0\leqslant z\leqslant 3 \right \}$

Rozwiązanie

Ponieważ granice całkowania są stałe, więc kolejność ich rozmieszczenia na całkach jest dowolona. Należy jedynie pamiętać o odpowiedniej kolejności różniczek.

$\dpi{120} \underset{D\; \; \; \: }{\iiint_{\, }^{\, }}\left ( x+y+z \right )d\sigma =\int_{{\color{Blue} 0}}^{{\color{Blue} 3}}\int_{{\color{Green} 0}}^{{\color{Green} 2}}\int_{{\color{Red} 0}}^{{\color{Red} 1}}\left ( x+y+z \right ){\color{Red} dx}\, {\color{Green} dy}\, {\color{Blue} dz}=$

Najpierw całkujemy po zmiennej $\dpi{120} x$ , pozostałe zmienne traktujemy jak stałe.

$\dpi{120} =\int_{0}^{3}\int_{0}^{2}\left [ \frac{x^{2}}{2} +xy+xz\right ]_{0}^{1}dy\, dz=$

$\dpi{120} =\int_{0}^{3}\int_{0}^{2}\left ( \frac{1^{2}}{2} +1\cdot y+1\cdot z-\overset{=0}{\overbrace{\frac{0^{2}}{2} -0\cdot y-0\cdot z}}\right )dy\, dz=$

$\dpi{120} =\int_{0}^{3}\int_{0}^{2}\left ( \frac{1}{2}+y+z \right )dy\, dz=$

Teraz całkujemy po zmiennej $\dpi{120} y$ , zmienną $\dpi{120} z$ traktując jak stałą:

$\dpi{120} =\int_{0}^{3}\left [ \frac{1}{2}y +\frac{y^{2}}{2}+yz\right ]_{0}^{2}dz=$

$\dpi{120} =\int_{0}^{3}\left ( \frac{1}{2}\cdot 2 +\frac{2^{2}}{2}+2\cdot z-\overset{=0}{\overbrace{\frac{1}{2}\cdot 0 -\frac{0^{2}}{2}-0\cdot z}}\right )dz=$

$\dpi{120} =\int_{0}^{3}\left ( 1+2+2z \right )dx=\int_{0}^{3}\left ( 3+2z \right )dz=$

$\dpi{120} =\left [ 3z+2\cdot \frac{z^{2}}{2} \right ]_{0}^{3}=\left [ 3z+z^{2} \right ]_{0}^{3}=$

$\dpi{120} =3\cdot 3+3^{2}-3\cdot 0-0^{2}=18$

Pokaż rozwiązanie

Zwiń

2) $\dpi{120} \underset{D\; \; \; \: }{\iiint_{\, }^{\, }}y \cos \left ( z+x \right ) d\sigma ,\; \: D=\left \{ 0\leqslant x\leqslant \frac{\pi }{4},\: 2\leqslant y\leqslant 4,\: 0\leqslant z\leqslant \frac{\pi }{2} \right \}$

Rozwiązanie

Ponieważ granice całkowania są stałe, więc kolejność ich rozmieszczenia na całkach jest dowolona. Należy jedynie pamiętać o odpowiedniej kolejności różniczek.

$\dpi{120} \underset{D\; \; \; \: }{\iiint_{\, }^{\, }}y \cos \left ( z+x \right ) d\sigma =\int_{{\color{Red} 0}}^{\frac{{\color{Red} \pi} }{{\color{Red} 4}}}\int_{{\color{Green} 2}}^{{\color{Green} 4}}\int_{{\color{Blue} 0}}^{\frac{{\color{Blue} \pi} }{{\color{Blue} 2}}}y\cos \left ( z+x \right ){\color{Blue} dz}\, {\color{Green} dy}\, {\color{Red} dx}=$

Całkujemy po zmiennej $\dpi{120} z$ . Wykorzystujemy wzór:

$\dpi{120} \int \cos \left ( ax+b \right )dx=\frac{1}{a}\sin \left ( ax+b \right )$

Są tutaj częste błędy. Pamiętajmy całkujemy po $\dpi{120} z$ , przy którym współczynnik $\dpi{120} a=1$ , $\dpi{120} x$ w tym przypadku jest stałą oznaczoną we wzorze przez $\dpi{120} b$ . Zatem:

$\dpi{120} =\int_{0}^{\frac{\pi }{4}}\int_{2}^{4}\left [ y\sin \left ( z+x \right ) \right ]_{0}^{\frac{\pi }{2}}dy\: dx=$

$\dpi{120} =\int_{0}^{\frac{\pi }{4}}\int_{2}^{4}\left [ y\sin \left ( \frac{\pi }{2}+x \right )- y\sin \left ( 0+x \right )\right ]dy\, dx=$

Ze wzoru redukcyjnego $\dpi{120} \sin \left ( \frac{\pi }{2}+x \right )=\cos x$ . Zatem:

$\dpi{120} =\int_{0}^{\frac{\pi }{4}}\int_{2}^{4}\left ( y\cos x- y\sin x\right )dy\, dx=$

$\dpi{120} =\int_{0}^{\frac{\pi }{4}}\int_{2}^{4}y\left ( \cos x- \sin x\right )dy\, dx=$

Całkujemy po zmiennej $\dpi{120} y$ :

$\dpi{120} =\int_{0}^{\frac{\pi }{4}}\left ( \cos x- \sin x\right )\cdot \left [ \frac{y^{2}}{2} \right ]_{2}^{4} dx=$

$\dpi{120} =\int_{0}^{\frac{\pi }{4}}\left ( \cos x- \sin x\right )\cdot \overset{=6}{\overbrace{\left ( \frac{4^{2}}{2}-\frac{2^{2}}{2} \right )}} dx=$

$\dpi{120} =6\int_{0}^{\frac{\pi }{4}}\left ( \cos x-\sin x \right )dx=$

Ostatnie całkowanie po $\dpi{120} x$ :

$\dpi{120} =6\cdot \left [ \sin x+\cos x \right ]_{0}^{\frac{\pi }{4}}=$

$\dpi{120} =6\cdot \left ( \sin \frac{\pi }{4}+\cos \frac{\pi }{4} -\sin 0-\cos 0\right )=$

$\dpi{120} =6\cdot \left ( \frac{\sqrt{2}}{2} +\frac{\sqrt{2}}{2}-0-1\right )=$

$\dpi{120} =6\cdot \left ( \sqrt{2}-1 \right )$

Pokaż rozwiązanie

Zwiń

3) $\dpi{120} \underset{D\; \; \; \: }{\iiint_{\, }^{\, }}2xe^{x^{2}+y+z}d\sigma ,\; \: D=\left \{ -1\leqslant x\leqslant 0,\: -1\leqslant y\leqslant 0,\: -1\leqslant z\leqslant 0 \right \}$

Rozwiązanie

Ponieważ granice całkowania są stałe, więc kolejność ich rozmieszczenia na całkach jest dowolna. Należy jedynie pamiętać o odpowiedniej kolejności różniczek.

$\dpi{120} \underset{D\; \; \; \: }{\iiint_{\, }^{\, }}2xe^{x^{2}+\, y+z}d\sigma =\int_{-1}^{0}\int_{-1}^{0}\int_{-1}^{0}2xe^{x^{2}+y+z}dy\, dz\, dx=$

$\dpi{120} =\int_{-1}^{0}\int_{-1}^{0}\int_{-1}^{0}2x\cdot e^{x^{2}}\cdot e^{y}\cdot e^{z}dy\, dz\, dx=$

$\dpi{120} =\int_{-1}^{0}\int_{-1}^{0}2x\cdot e^{x^{2}}\cdot e^{z}\int_{-1}^{0}e^{y}\, dy\, dz\, dx=$

$\dpi{120} =\int_{-1}^{0}\int_{-1}^{0}2x\cdot e^{x^{2}}\cdot e^{z}\cdot \left [e^{y} \right ]_{-1}^{0}\, dz\, dx=$

$\dpi{120} =\int_{-1}^{0}\int_{-1}^{0}2x\cdot e^{x^{2}}\cdot e^{z}\cdot \overset{1-e^{-1}}{\overbrace{\left (e^{0}-e^{-1} \right )}}\, dz\, dx=$

$\dpi{120} =\left ( 1-e^{-1} \right )\int_{-1}^{0}2x\cdot e^{x^{2}}\int_{-1}^{0} e^{z}\right )\, dz\, dx=$

$\dpi{120} =\left ( 1-e^{-1} \right )\int_{-1}^{0}2x\cdot e^{x^{2}} \cdot \left [e^{z} \right ]_{-1}^{0}\right )\, dx=$

$\dpi{120} =\left ( 1-e^{-1} \right )\int_{-1}^{0}2x\cdot e^{x^{2}} \cdot \overset{1-e^{-1}}{\overbrace{\left (e^{0}-e^{-1} \right )}}\, dx=$

$\dpi{120} =\left ( 1-e^{-1} \right )^{2}\int_{-1}^{0}2x\cdot e^{x^{2}}\, dx=$

Ostatnią całkę liczymy przez podstawienie, najpierw całkę nieoznaczoną, aby nie zmieniać granic całkowania:

$\dpi{120} \int 2x\cdot e^{x^{2}}\, dx=\begin{Bmatrix} x^{2}=t\\ 2xdx=dt\\ dx=\frac{dt}{2x} \end{Bmatrix}=\int 2x\cdot e^{t}\cdot \frac{dt}{2x}=$

$\dpi{120} =\int e^{t}\, dt=e^{t}\: \overset{t=x^{2}}{=}e^{x^{2}}$

Wracamy do naszej całki oznaczonej:

$\dpi{120} =\left ( 1-e^{-1} \right )^{2}\left [ e^{x^{2}} \right ]_{-1}^{0}=$

$\dpi{120} =\left ( 1-e^{-1} \right )^{2}\left [ e^{0^{2}}-e^{\left ( -1 \right )^{2}} \right ]=$

$\dpi{120} =\left ( 1-e^{-1} \right )^{2}\left (1-e \right )$

Pokaż rozwiązanie

Zwiń

Zadanie 2. Obliczyć całkę potrójną $\dpi{120} \large \underset{D\; \; \; \: }{\iiint_{\, }^{\, }}z\, d\sigma$ w obszarze normalnym:

1) $\dpi{120} D=\left \{ 0\leqslant x\leqslant 1,\, x\leqslant y\leqslant 1,\, x\leqslant z\leqslant y\right \}$

Rozwiązanie

Spójrzmy na granice obszaru $\dpi{120} D$ . Nie są stałe, więc ich kolejność na całkach nie jest dowolna. Pamiętajmy, że na zewnętrznej całce musi być stała granica całkowania, czyli u nas $\dpi{120} 0\leqslant x\leqslant 1$ , na następnych zwiększamy ilość zmiennych, a więc najpierw $\dpi{120} x\leqslant y\leqslant 1$ , a następnie $\dpi{120} x\leqslant z\leqslant y$ . Otrzymujemy:

$\dpi{120} \underset{D\; \; \; \: }{\iiint_{\, }^{\, }}z\, d\sigma=\int_{{\color{Red} 0}}^{{\color{Red} 1}}\int_{{\color{Green} x}}^{{\color{Green} 1}}\int_{{\color{Blue} x}}^{{\color{Blue} y}}z\, {\color{Blue} dz}\, {\color{Green} dy}\, {\color{Red} dx}=$

Najpierw całkujemy po zmiennej $\dpi{120} z$ :

$\dpi{120} =\int_{0}^{1}\int_{x}^{1}\left [ \frac{z^{2}}{2} \right ]_{x}^{y}dy\, dx=$

$\dpi{120} =\int_{0}^{1}\int_{x}^{1}\left ( \frac{y^{2}}{2} -\frac{x^{2}}{2}\right )dy\, dx=$

$\dpi{120} =\frac{1}{2}\int_{0}^{1}\int_{x}^{1}\left (y^{2} -x^{2}\right )dy\, dx=$

Całkujemy po zmiennej $\dpi{120} y$ :

$\dpi{120} =\frac{1}{2}\int_{0}^{1}\left [ \frac{y^{3}}{3} -x^{2}y\right ]_{x}^{1}dx=$

$\dpi{120} =\frac{1}{2}\int_{0}^{1}\left ( \frac{1^{3}}{3} -x^{2}\cdot 1-\frac{x^{3}}{3}+x^{2}\cdot x\right )dx=$

$\dpi{120} =\frac{1}{2}\int_{0}^{1}\left ( \frac{1}{3}-x^{2}+\frac{2}{3}x^{3} \right )dx=$

$\dpi{120} =\frac{1}{2}\cdot \left [ \frac{1}{3}x- \frac{x^{3}}{3} +\frac{2}{3}\cdot \frac{x^{4}}{4}\right ]_{0}^{1}=$

$\dpi{120} =\frac{1}{2}\cdot \left ( \frac{1}{3}\cdot 1- \frac{1^{3}}{3} +\frac{2}{3}\cdot \frac{1^{4}}{4}\right )=$

$\dpi{120} =\frac{1}{2}\cdot \left ( \frac{1}{3}-\frac{1}{3}+\frac{1}{6} \right )=\frac{1}{12}$

Pokaż rozwiązanie

Zwiń

2) $\dpi{120} D=\left \{ z\leqslant x\leqslant y,\, 0\leqslant y\leqslant 1,\, 0\leqslant z\leqslant y\right \}$

Rozwiązanie

Spójrzmy na granice obszaru $\dpi{120} D$ . Nie są stałe, więc ich kolejność na całkach nie jest dowolna. Pamiętajmy, że na zewnętrznej całce musi być stała granica całkowania, czyli u nas $\dpi{120} 0\leqslant y\leqslant 1$ , na następnych zwiększamy ilość zmiennych, a więc najpierw $\dpi{120} 0\leqslant z\leqslant y$ , a następnie $\dpi{120} z\leqslant x\leqslant y$ . Otrzymujemy:

$\dpi{120} \underset{D\; \; \; \: }{\iiint_{\, }^{\, }}z\, d\sigma=\int_{{\color{Red} 0}}^{{\color{Red} 1}}\int_{{\color{Green} 0}}^{{\color{Green} y}}\int_{{\color{Blue} z}}^{{\color{Blue} y}}z\, {\color{Blue} dx}\, {\color{Green} dz}\, {\color{Red} dy}=$

Najpierw całkujemy po zmiennej $\dpi{120} x$ , pozostałe traktując jak parametry:

$\dpi{120} =\int_{{\color{Red} 0}}^{{\color{Red} 1}}\int_{{\color{Green} 0}}^{{\color{Green} y}}z\cdot \left [x \right ]_{{\color{Blue} z}}^{{\color{Blue} y}}\, {\color{Green} dz}\, {\color{Red} dy}=$

$\dpi{120} =\int_{{\color{Red} 0}}^{{\color{Red} 1}}\int_{{\color{Green} 0}}^{{\color{Green} y}}z\cdot \left ({\color{Blue} y}-{\color{Blue} z }\right )\, {\color{Green} dz}\, {\color{Red} dy}=$

$\dpi{120} =\int_{{\color{Red} 0}}^{{\color{Red} 1}}\int_{{\color{Green} 0}}^{{\color{Green} y}}\left (zy-z^{2} \right )\, {\color{Green} dz}\, {\color{Red} dy}=$

Całkujemy po zmiennej $\dpi{120} z$ :

$\dpi{120} =\int_{{\color{Red} 0}}^{{\color{Red} 1}}\left [ \frac{z^{2}}{2} \cdot y-\frac{z^{3}}{3}\right ]_{{\color{Green} 0}}^{{\color{Green} y}}\, {\color{Red} dy}=$

$\dpi{120} =\int_{{\color{Red} 0}}^{{\color{Red} 1}}\left ( \frac{{\color{Green} y}^{2}}{2} \cdot y-\frac{{\color{Green} y}^{3}}{3}-\frac{{\color{Green} 0}^{2}}{2}\cdot y+\frac{{\color{Green} 0}^{3}}{3}\right )\, {\color{Red} dy}=$

$\dpi{120} =\int_{{\color{Red} 0}}^{{\color{Red} 1}}\left ( \frac{y^{3}}{2}-\frac{y^{3}}{3} \right )\,{\color{Red} dy }=\int_{{\color{Red} 0}}^{{\color{Red} 1}}\frac{y^{3}}{6}\,{\color{Red} dy }=$

Ostatnie całkowanie po zmiennej $\dpi{120} y$ :

$\dpi{120} =\left [ \frac{1}{6}\cdot \frac{y^{4}}{4} \right ]_{{\color{Red} 0}}^{{\color{Red} 1}}=\frac{1}{24}\cdot \left ( {\color{Red} 1}^{4}-{\color{Red} 0}^{4} \right )=\frac{1}{24}$

Pokaż rozwiązanie

Zwiń

3) $\dpi{120} D=\left \{ 0\leqslant x\leqslant z,\, z+x\leqslant y\leqslant z-x,\, 0\leqslant z\leqslant 1\right \}$

Rozwiązanie

Spójrzmy na granice obszaru $\dpi{120} D$ . Nie są stałe, więc ich kolejność na całkach nie jest dowolna. Pamiętajmy, że na zewnętrznej całce musi być stała granica całkowania, czyli u nas $\dpi{120} 0\leqslant z\leqslant 1$ , na następnych zwiększamy ilość zmiennych, a więc najpierw $\dpi{120} 0\leqslant x\leqslant z$ , a następnie $\dpi{120} z+x\leqslant y\leqslant z-x$ . Otrzymujemy:

$\dpi{120} \underset{D\; \; \; \: }{\iiint_{\, }^{\, }}z\, d\sigma=\int_{{\color{Red} 0}}^{{\color{Red} 1}}\int_{{\color{Green} 0}}^{{\color{Green} z}}\int_{{\color{Blue} z+x}}^{{\color{Blue} z-x}}z\, {\color{Blue} dy}\, {\color{Green} dx}\, {\color{Red} dz}=$

Najpierw całkujemy po zmiennej $\dpi{120} y$ :

$\dpi{120} =\int_{{\color{Red} 0}}^{{\color{Red} 1}}\int_{{\color{Green} 0}}^{{\color{Green} z}}z\cdot \left [ y \right ]_{{\color{Blue} z+x}}^{{\color{Blue} z-x}}\, {\color{Green} dx}\, {\color{Red} dz}=$

$\dpi{120} =\int_{{\color{Red} 0}}^{{\color{Red} 1}}\int_{{\color{Green} 0}}^{{\color{Green} z}}z\cdot \left [ {\color{Blue} z-x}-\left ( {\color{Blue} z+x} \right ) \right ]\, {\color{Green} dx}\, {\color{Red} dz}=$

$\dpi{120} =\int_{{\color{Red} 0}}^{{\color{Red} 1}}\int_{{\color{Green} 0}}^{{\color{Green} z}}z\cdot \left ( -2x \right )\, {\color{Green} dx}\, {\color{Red} dz}=$

Całkujemy po zmiennej $\dpi{120} x$ :

$\dpi{120} =\int_{{\color{Red} 0}}^{{\color{Red} 1}}-2z\cdot \left [ \frac{x^{2}}{2} \right ]_{{\color{Green} 0}}^{{\color{Green} z}}\, {\color{Red} dz}=$

$\dpi{120} =\int_{{\color{Red} 0}}^{{\color{Red} 1}}-2z\cdot \left [ \frac{{\color{Green} z}^{2}}{2}-\frac{{\color{Green} 0}^{2}}{2} \right ]\, {\color{Red} dz}=$

$\dpi{120} =\int_{{\color{Red} 0}}^{{\color{Red} 1}}\left ( -z^{3} \right )\, {\color{Red} dz}=$

Ostatnie całkowanie po zmiennej $\dpi{120} z$ :

$\dpi{120} =\left [ -\frac{z^{4}}{4} \right ]_{{\color{Red} 0}}^{{\color{Red} 1}}=-\frac{{\color{Red} 1}^{4}}{4}+\frac{{\color{Red} 0}^{4}}{4}=-\frac{1}{4}$

Pokaż rozwiązanie

Zwiń

Zadanie 3. Obliczyć całki potrójne:

1) $\dpi{120} \underset{D\; \; \; \: }{\iiint_{\, }^{\, }}2z\, d\sigma,\; \; D=\left \{ \left ( x,y \right )\in G;\: \sqrt{2-x}\leqslant z\leqslant \sqrt{6+y} \right \}$ , a $\dpi{120} \large G$ oznacza trójkąt o wierzchołkach $\dpi{120} \left ( 0,0 \right ),\: \left ( 0,2 \right ),\: \left ( 2,0 \right )$

Rozwiązanie

Najpierw narysujmy obszar $\dpi{120} G$ .

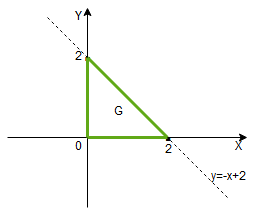
Obszar ten opiszemy nierównościami jako:

$\dpi{120} {\color{Red} 0}\leqslant x\leqslant {\color{Red} 2}$

$\dpi{120} {\color{Green} 0}\leqslant y\leqslant {\color{Green} -x+2}$

Wróćmy do całki potrójnej:

$\dpi{120} \underset{D\; \; \; \: }{\iiint_{\, }^{\, }}2z\, d\sigma=\int_{{\color{Red} 0}}^{{\color{Red} 2}}\int_{{\color{Green} 0}}^{{\color{Green} -x+2}}\int_{{\color{Blue} \sqrt{ 2-x}}}^{{\color{Blue} \sqrt{6+y}}}2z\, {\color{Blue} dz}\, {\color{Green} dy}\, {\color{Red} dx}=$

Najpierw całkujemy po zmiennej $\dpi{120} z$ :

$\dpi{120} =\int_{{\color{Red} 0}}^{{\color{Red} 2}}\int_{{\color{Green} 0}}^{{\color{Green} -x+2}}\left [2\cdot \frac{z^{2}}{2} \right ]_{{\color{Blue} \sqrt{2-x}}}^{{\color{Blue} \sqrt{6+y}}}\, {\color{Green} dy}\, {\color{Red} dx}=$

$\dpi{120} =\int_{{\color{Red} 0}}^{{\color{Red} 2}}\int_{{\color{Green} 0}}^{{\color{Green} -x+2}}\left [ \left ({\color{Blue} \sqrt{6+y}} \right )^{2}-\left ({\color{Blue} \sqrt{2-x}} \right )^{2} \right ]\, {\color{Green} dy}\, {\color{Red} dx}=$

$\dpi{120} =\int_{{\color{Red} 0}}^{{\color{Red} 2}}\int_{{\color{Green} 0}}^{{\color{Green} -x+2}}\left ( 4+y+x\right )\, {\color{Green} dy}\, {\color{Red} dx}=$

Całkujemy po zmiennej $\dpi{120} y$ :

$\dpi{120} =\int_{{\color{Red} 0}}^{{\color{Red} 2}}\left [ 4y+\frac{y^{2}}{2}+xy\right ]_{{\color{Green} 0}}^{{\color{Green} -x+2}}\, {\color{Red} dx}=$

$\dpi{120} =\int_{{\color{Red} 0}}^{{\color{Red} 2}}\left [ 4\cdot \left ( {\color{Green} -x+2} \right )+\frac{\left ( {\color{Green} -x+2} \right )^{2}}{2}+x\cdot \left ( {\color{Green} -x+2 }\right )-{\color{Green} 0}\right ]\, {\color{Red} dx}=$