Liczby zespolone, potęgowanie, wzory

Wzór de Moivre’a:

$wzór Moivre'a (potęgowanie liczb zespolonych)$

Fakty potrzebne do potęgowania liczb zespolonych:

1) funkcje sinus oraz cosinus są okresowe o okresie $\dpi{120} 2\pi$

2) wzory redukcyjne (minimalny zestaw):

$\dpi{120} \sin \left ( \pi -\alpha \right )=\sin \alpha$	$\dpi{120} \sin \left ( \pi +\alpha \right )=-\sin \alpha$	$\dpi{120} \sin \left ( 2\pi -\alpha \right )=-\sin \alpha$
$\dpi{120} \cos \left ( \pi -\alpha \right )=-\cos \alpha$	$\dpi{120} \cos \left ( \pi +\alpha \right )=-\cos \alpha$	$\dpi{120} \cos \left ( 2\pi -\alpha \right )=\cos \alpha$

3) wszystkie wiadomości z zakładki Wzory – postać trygonometryczna liczby zespolonej

Algorytm podnoszenia liczby zespolonej $\dpi{120} z=a+bi$ do potęgi $\dpi{120} n\in \mathbb{N}$

1. Sprowadzamy liczbę do postaci trygonometrycznej (patrz algorytm sprowadzania liczby zespolonej do postaci trygonometrycznej w zakładce Wzory w temacie Postać trygonometryczna tutaj).

2. Wykorzystujemy wzór de Moivre’a

$\dpi{120} z^{n}=\left | z \right |^{n}\cdot \left ( \cos \left ( n\varphi \right ) +i\, \sin \left ( n\varphi \right )\right ),\, n\in \mathbb{N}$

wstawiając za 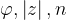$\dpi{120} \varphi ,\left | z \right |,n$ odpowiednie wartości z punktu 1.

3. Mnożymy (ewentualnie skracamy) iloczyn 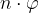$\dpi{120} n\cdot \varphi$ . Możemy otrzymać ułamki o dużych wartościach w liczniku.

4. Wyłączamy całości z otrzymanego ułamka z punktu 3.

5. Opuszczamy największą liczbę parzystą zawartą w liczbie mieszanej otrzymanej w punkcie 4. Zostaje liczba mniejsza od 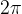$\dpi{120} 2\pi$ .

6. Jeżeli dostaliśmy liczbę mniejszą bądź równą 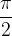$\dpi{120} \frac{\pi }{2}$ odczytujemy wartości sinusów i cosinusów z tabeli wartości funkcji trygonometrycznych. Koniec zadania.

7. Jeżeli dostaliśmy liczbę większą od 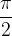$\dpi{120} \frac{\pi }{2}$ , musimy zastosować wzory redukcyjne.

a) ustalamy ćwiartkę, do której należy nasz kąt

b) zapisujemy go tak, aby móc skorzystać ze wzorów redukcyjnych

c) stosujemy wzory redukcyjne

8) Odczytujemy wartości sinusów i cosinusów z tabeli wartości funkcji trygonometrycznych. Koniec zadania.

Pokaż algorytm

Zwiń

Zapraszamy do zadań! tutaj