Przed rozpoczęciem rozwiązywania zadań warto zapoznać się z definicjami i własnościami dotyczącymi rachunku zbiorów w zakładce Teoria tutaj lub w skróconej wersji w zakładce Wzory tutaj. W rozwiązaniach zadań będzie wykorzystywana wiedza z zakresu praw logicznych, zob. tutaj.
Zadanie 1. Dane są przedziały: . Wyznaczyć zbiory:
1)
Rozwiązanie
Przedstawmy zbiory na osi liczbowej:
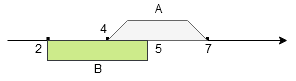
Otrzymujemy:
– elementy należące do zbioru
lub do zbioru
– elementy należące do zbioru
i do zbioru
, tzw. część wspólna
– elementy należące do zbioru
i nie należące do zbioru
– elementy należące do zbioru
i nie należące do zbioru
Zauważmy, że dla różnicy symetrycznej mamy:
2)
Rozwiązanie Przedstawmy zbiory na osi liczbowej: Otrzymujemy: Zauważmy, że dla różnicy symetrycznej mamy: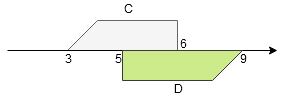
– elementy należące do zbioru
lub do zbioru
– elementy należące do zbioru
i do zbioru
, tzw. część wspólna
– elementy należące do zbioru
i nie należące do zbioru
– elementy należące do zbioru
i nie należące do zbioru
3)
Rozwiązanie Wykonajmy działania na zbiorach stopniowo. 1. Zatem 2. Zatem 3. Zatem 
.
.
![]()
. (należy do szarego
i nie należy do zielonego
)
4)
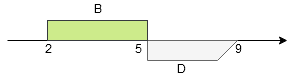
Rozwiązanie Wykonajmy działania na zbiorach stopniowo. 1. Zatem 2. Zatem 
.

. (należy do szarego
i nie należy do zielonego
)
Zadanie 2. Dowieść następujących praw rachunku zdań:
W dowodach będzie wykorzystywana wiedza z zakresu praw logicznych, zob. tutaj.
1) – prawo rozdzielności sumy zbiorów względem iloczynu zbiorów
Rozwiązanie
Niech element należy do lewej części zależności. Z definicji sumy zbiorów mamy:
Następnie z definicji iloczynu zbiorów otrzymujemy:
Korzystamy z prawa logicznego :
Wyrażenie oznacza, że
, zaś wyrażenie
oznacza, że
. Otrzymujemy:
To z kolei oznacza, że
Pokazaliśmy, że dowolny element należy do prawej strony zależności. Co było do pokazania.
2)
Rozwiązanie Niech element Wyrażenie Następnie z definicji sumy zbiorów otrzymujemy: Korzystamy z prawa de Morgana Korzystamy z prawa łączności koniunkcji Wyrażenie To z kolei oznacza, że Pokazaliśmy, że dowolny element
należy do lewej części zależności. Z definicji różnicy zbiorów mamy:
zapiszmy jako
. (Tutaj częste błędy)
:
oraz możemy powtórzyć wyrażenie
:
oznacza, że
, zaś wyrażenie
oznacza, że
. Otrzymujemy:
należy do prawej strony zależności. Co było do pokazania.
3)
Rozwiązanie Niech element Z definicji sumy zbiorów otrzymujemy: Korzystamy z prawa rozdzielności Wyrażenie To z kolei oznacza, że Pokazaliśmy, że dowolny element
należy do lewej części zależności. Z definicji różnicy zbiorów mamy:
:
oznacza, że
, zaś wyrażenie
oznacza, że
. Otrzymujemy:
należy do prawej strony zależności. Co było do pokazania.
4)
Rozwiązanie Niech element Wyrażenie Ponownie z różnicy zbiorów otrzymujemy: Stosujemy prawo de Morgana do nawiasu kwadratowego Korzystamy z prawa rozdzielności Wyrażenie To z kolei oznacza, że Pokazaliśmy, że dowolny element
należy do lewej części zależności. Z definicji różnicy zbiorów mamy:
zapiszmy jako
:
:
:
oznacza, że
, zaś wyrażenie
oznacza, że
. Otrzymujemy:
należy do prawej strony zależności. Co było do pokazania.
Zadanie 3. Sprawdzić, czy dla dowolnych zbiorów zachodzi:
Jest to inny rodzaj dowodu niż w poprzednim zadaniu.
1) jeżeli , to
Rozwiązanie
Tworzymy na podstawie powyższego twierdzenia prawo logiczne. Zastępujemy odpowiednio znaki: równości – równoważnością, iloczyn – koniunkcją, zawieranie – implikacją. Jako główny znak twierdzenia stawiamy również implikację, gdyż mamy konstrukcję: Jeżeli …, to…. Jako zdania przyjmujemy:
Otrzymujemy:
Dowodzimy powyższe prawo dowolną metodą poznaną wcześniej. Patrz tutaj. My sprawdzimy je za pomocą tabeli zerojedynkowej.
| 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Pokazaliśmy, że jest to tautologia, więc nasze twierdzenie dotyczące zbiorów jest prawdziwe.
2) jeżeli , to
Rozwiązanie
Tworzymy na podstawie powyższego twierdzenia prawo logiczne. Zastępujemy odpowiednio znaki: równości – równoważnością, sumy – alternatywą, zawieranie – implikacją, uważajmy na różnicę. Jako główny znak twierdzenia stawiamy również implikację, gdyż mamy konstrukcję: Jeżeli …, to…. Jako zdania przyjmujemy:
Otrzymujemy:
Dowodzimy powyższe prawo dowolną metodą poznaną wcześniej. Patrz tutaj. My sprawdzimy je za pomocą tabeli zerojedynkowej.
| 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 |
Pokazaliśmy, że jest to tautologia, więc nasze twierdzenie dotyczące zbiorów jest prawdziwe.
3) jeżeli , to
Rozwiązanie Tworzymy na podstawie powyższego twierdzenia prawo logiczne. Zastępujemy odpowiednio znak zawierania – implikacją, uważajmy na różnicę. Jako główny znak twierdzenia stawiamy również implikację, gdyż mamy konstrukcję: Jeżeli …, to…. Jako zdania Otrzymujemy: Dowodzimy powyższe prawo dowolną metodą poznaną wcześniej. Patrz tutaj. My sprawdzimy je za pomocą tabeli zerojedynkowej. Pokazaliśmy, że jest to tautologia, więc nasze twierdzenie dotyczące zbiorów jest prawdziwe.
przyjmujemy:
0
0
0
1
1
1
0
0
1
1
0
0
1
1
1
1
1
1
1
1
0
1
0
1
1
0
0
0
1
1
1
0
0
0
0
1
0
0
1
1
0
1
1
1
1
0
0
1
1
1
1
1
0
1
0
0
0
0
1
1
1
0
1
0
0
1
1
0
0
1
1
1
1
1
0
0
0
0
1
1
Zadanie 4. Znaleźć: , gdzie:
1)
Rozwiązanie
Zobaczmy najpierw jak wyglądają zbiory . Zakładamy, że
. Otrzymujemy:
Zaznaczmy je na osi:

Zatem:
Rozszerzmy teraz zbiór wskaźników na zbiór
.
2)
Rozwiązanie Zobaczmy najpierw jak wyglądają zbiory Zatem: Rozszerzmy teraz zbiór wskaźników Wówczas:
. Zakładamy, że
. Otrzymujemy:
na zbiór
. Wypiszmy kilka zbiorów:
, itd.