Wyznacznik macierzy (zadania) - WYZNACZNIK

Mamy 7 zadań. Zadanie 1 i 2 dotyczą wyznaczników macierzy 2 i 3 stopnia. Liczymy je bez użycia rozwinięcia Laplace’a (metodą Sarrusa). W zadaniu 2 wyznaczniki są ”włożone” w równanie bądź nierówność. W zadaniu 3 wkracza rozwinięcie Laplace’a. Kolejność podpunktów w zadaniu jest bardzo istotna. Zaczynamy od przykładów łatwych, kończymy na przykładzie dosyć długim. Prosimy nie omijać podpunktów, gdyż prawie w każdym pojawia się nowa ważna informacja. Zadania od 4 do 7 są niestandardowe. Mimo wszystko warto do nich zajrzeć, bo rozwiązania są bardzo krótkie. Wykorzystują podstawowe własności wyznaczników. Nadają się na pytania testowe. Przed przystąpieniem do zadań warto zapoznać się z zakładkami Teoria tutaj i Wzory tutaj.

Zadanie 1. Obliczyć wartości wyznaczników:

a) $\dpi{120} \begin{vmatrix} 2 & 5\\ -2& 3 \end{vmatrix}$ ,

Rozwiązanie

$\dpi{120} \begin{vmatrix}{\color{Red} 2} & {\color{Blue} 5}\\ {\color{Blue} -2} & {\color{Red} 3} \end{vmatrix}={\color{Red} 2}\cdot {\color{Red} 3}-{\color{blue} 5}\cdot ({\color{Blue} -2})=6+10=16$

Pokaż rozwiązanie

Zwiń

b) $\dpi{120} \begin{vmatrix} -4 & 6\\ -3 & -1 \end{vmatrix}$ ,

Rozwiązanie

$\dpi{120} \begin{vmatrix} {\color{Red} -4} & {\color{Blue} 6} \\ {\color{Blue} -3}& {\color{Red} -1} \end{vmatrix}={\color{Red} -4}\cdot ({\color{Red} -1})-{\color{Blue} 6} \cdot ({\color{Blue} -3})=4+18=22$

Pokaż rozwiązanie

Zwiń

c) $\dpi{120} \begin{vmatrix} -1 & 2 &1 \\ 3 & -1 &2 \\ 1& -2& 3 \end{vmatrix}$ ,

Rozwiązanie

Stosujemy metodę Sarrusa. Dopisujemy za macierzą dwie pierwsze kolumny. Tworzymy przekątne: trzy w prawą stronę zaczynając od -1 dalej od 2 i od 1. Mnożymy elementy każdej przekątnej, a następnie sumujemy. Następnie trzy przekątne w lewą stronę poczynając od 2, -1 i 1. Mnożymy elementy na przekątnych. Zmieniamy znaki w trzech ostatnich iloczynach i je sumujemy.

$\dpi{120} \begin{vmatrix} -1 & 2 & 1\\ 3&-1 & 2\\ 1 &-2 & 3 \end{vmatrix}\begin{matrix} -1 &2 \\ 3&-1 \\ 1 &-2 \end{matrix}=$

$\dpi{120} =-1\cdot (-1)\cdot 3+2\cdot 2\cdot 1+1\cdot 3\cdot (-2)-2\cdot 3\cdot 3-(-1)\cdot 2\cdot (-2)-1\cdot (-1)\cdot 1=$

$\dpi{120} =3+4-6-18-4+1=-20.$

Pokaż rozwiązanie

Zwiń

d) $\dpi{120} \begin{vmatrix} 12 & 6 &-4 \\ 6 & 4 & 4\\ 3& 2 & 8 \end{vmatrix}$ ,

Rozwiązanie

Stosujemy metodę Sarrusa. Dopisujemy za macierzą dwie pierwsze kolumny. Tworzymy odpowiednie przekątne.

$\dpi{120} \begin{vmatrix} 12 & 6 & -4\\ 6&4 &4 \\ 3 & 2 & 8 \end{vmatrix}\begin{matrix} 12 &6 \\ 6& 4\\ 3& 2 \end{matrix}=$

$\dpi{120} =12\cdot 4\cdot 8+6\cdot 4\cdot 3+(-4)\cdot 6\cdot 2-6\cdot6\cdot 8-12\cdot4\cdot 2-(-4)\cdot 4\cdot 3=$

$\dpi{120} =384+72-48-288-96+48=72$

Pokaż rozwiązanie

Zwiń

e) $\dpi{120} \begin{vmatrix} 1 & 2 & 1\\ 1 &0 &2 \\ 4 & 3 &5 \end{vmatrix}$ ,

Rozwiązanie

Stosujemy metodę Sarrusa. Dopisujemy za macierzą dwie pierwsze kolumny. Tworzymy odpowiednie przekątne.

$\dpi{120} \begin{vmatrix} 1 & 2 &1 \\ 1 &0 &2 \\ 4 & 3 & 5 \end{vmatrix}\begin{matrix} 1 &2 \\ 1 & 0\\ 4& 3 \end{matrix}=$

$\dpi{120} =1\cdot 0\cdot 5+2\cdot 2\cdot 4+1\cdot1\cdot 3-2\cdot 1\cdot 5-1\cdot 2\cdot 3-1\cdot 0\cdot 4=$

$\dpi{120} =0+16+3-10-6-0=3.$

Pokaż rozwiązanie

Zwiń

f) $\dpi{120} \begin{vmatrix} 1 & 2 & 3a\\ a& 5 &-1 \\ 2& a & 10 \end{vmatrix}$ ,

Rozwiązanie

Stosujemy metodę Sarrusa. Dopisujemy za macierzą dwie pierwsze kolumny. Tworzymy odpowiednie przekątne.

$\dpi{120} \begin{vmatrix} 1 & 2 & 3a\\ a & 5 &-1 \\ 2& a &10 \end{vmatrix}\begin{matrix} 1 &2 \\ a & 5\\ 2& a \end{matrix}=$

$\dpi{120} =1\cdot 5\cdot 10+2\cdot (-1)\cdot 2+3a\cdot a\cdot a-2\cdot a\cdot 10-1\cdot (-1)\cdot a-3a\cdot 5\cdot 2=$

$\dpi{120} =50-4+3a^{3}-20a+a-30a=3a^{3}-49a+46.$

Pokaż rozwiązanie

Zwiń

g) $\dpi{120} \begin{vmatrix} 1 &x & z\\ 1& x+y & z\\ 1& x & z+u \end{vmatrix}$ .

Rozwiązanie

$\dpi{120} \begin{vmatrix} 1 & x &z \\ 1& x+y & z\\ 1 & x &z+u \end{vmatrix}\begin{matrix} 1 &x \\ 1 &x+y \\ 1 & x \end{matrix}=$

$\dpi{120} =1\cdot (x+y)\cdot (z+u)+x\cdot z\cdot 1+z\cdot 1\cdot x-x\cdot 1\cdot (z+u)-1\cdot z\cdot x-z\cdot (x+y)\cdot 1=$

$\dpi{120} ={\color{Red} xz}{\color{Blue} +xu}{\color{DarkGreen} +yz}+yu{\color{Red} +xz+xz-xz}{\color{Blue} -xu}{\color{Red} -zx-zx}{\color{DarkGreen} -zy}=yu.$

Pokaż rozwiązanie

Zwiń

Zadanie 2. Rozwiązać równanie lub nierówność:

a) $\dpi{120} \begin{vmatrix} -x & 1 & x\\ 0& -x & -1\\ x & 1 & -x \end{vmatrix}=-2$ ,

Rozwiązanie

Najpierw obliczmy wyznacznik:

$\dpi{120} \begin{vmatrix} -x & 1& x\\ 0 &-x & -1\\ x &1 & -x \end{vmatrix}\begin{matrix} -x &1 \\ 0 & -x\\ x& 1 \end{matrix}=$

$\dpi{120} =-x\cdot (-x)\cdot (-x)+1\cdot (-1)\cdot x+x\cdot 0\cdot 1-1\cdot 0\cdot (-x)-(-x)\cdot (-1)\cdot 1-x\cdot (-x)\cdot x=$

$\dpi{120} =-x^{3}-x+0-0-x+x^{3}=-2x$

Wracamy do równania:

$\dpi{120} -2x=-2/:(-2)$

$\dpi{120} x=1.$

Pokaż rozwiązanie

Zwiń

b) $\dpi{120} \begin{vmatrix} 1 & 2 & 3\\ 1 & 3-x & 3\\ 1&2 &5+x \end{vmatrix}=0$ ,

Rozwiązanie

Liczymy wyznacznik:

$\dpi{120} \begin{vmatrix} 1 &2 &3 \\ 1 &3-x &3 \\ 1 &2 & 5+x \end{vmatrix}\begin{matrix} 1 & 2\\ 1&3-x \\ 1& 2 \end{matrix}=$

$\dpi{120} =1\cdot (3-x)\cdot (5+x)+2\cdot 3\cdot 1+3\cdot 1\cdot 2-2\cdot 1\cdot (5+x)-1\cdot 3\cdot 2-3\cdot (3-x)\cdot 1=$

$\dpi{120} =15+3x-5x-x^{2}+6+6-10-2x-6-9+3x=-x^{2}-x+2$

Wracamy do równania:

$\dpi{120} -x^{2}-x+2=0$

$\dpi{120} \Delta =(-1)^{2}-4\cdot (-1)\cdot 2=1+8=9,\; \sqrt{\Delta }=3$

$\dpi{120} x_{1}=\frac{-(-1)-3}{2\cdot (-1)}=1,\: x_{2}=\frac{-(-1)+3}{2\cdot (-1)}=-2$

Rozwiązaniami równania są liczby $\dpi{120} x_{1}=1,\: x_{2}=-2.$

Pokaż rozwiązanie

Zwiń

c) $\dpi{120} \begin{vmatrix} x^{2} &3 &2 \\ x & -1 & 1\\ 0 & 1 & 4 \end{vmatrix}=0,$

Rozwiązanie

Liczymy wyznacznik:

$\dpi{120} \begin{vmatrix} x^{2} & 3 & 2\\ x& -1 &1 \\ 0 &1 &4 \end{vmatrix}\begin{matrix} x^{2} &3 \\ x&-1 \\ 0 &1 \end{matrix}=$

$\dpi{120} =x^{2}\cdot (-1)\cdot 4+3\cdot 1\cdot 0+2\cdot x\cdot 1-3\cdot x\cdot 4-x^{2}\cdot 1\cdot 1-2\cdot (-1)\cdot 0=$

$\dpi{120} =-4x^{2}+0+2x-12x-x^{2}+0=5x^{2}-10x$

Wracamy do równania:

$\dpi{120} -5x^{2}-10x=0/:(-5)$

$\dpi{120} x^{2}+2x=0$

$\dpi{120} x(x+2)=0\Rightarrow x_{1}=0\vee x_{2}=-2$

Rozwiązaniami są liczby $\dpi{120} x_{1}=0,x_{2}=-2.$

Pokaż rozwiązanie

Zwiń

d) $\dpi{120} \begin{vmatrix} x^{2} &4 & 9\\ x& 2 & 3\\ 1& 1 & 1 \end{vmatrix}> 0,$

Rozwiązanie

Liczymy wyznacznik:

$\dpi{120} \begin{vmatrix} x^{2} &4 &9 \\ x & 2 &3 \\ 1& 1 & 1 \end{vmatrix}\begin{matrix} x^{2} &4 \\ x &2 \\ 1 & 1 \end{matrix}=$

$\dpi{120} =x^{2}\cdot 2\cdot 1+4\cdot 3\cdot 1+9\cdot x\cdot 1-4\cdot x\cdot 1 -x^{2}\cdot 3\cdot 1-9\cdot 2\cdot 1=$

$\dpi{120} =2x^{2}+12+9x-4x-3x^{2}-18=-x^{2}+5x-6$

Wracamy do nierówności:

$\dpi{120} -x^{2}+5x-6> 0$

$\dpi{120} \Delta =25-4\cdot (-1)\cdot (-6)=25-24=1,\; \sqrt{\Delta }=1$

$\dpi{120} x_{1}=\frac{-5-1}{2\cdot (-1)}=3,\: x_{2}=\frac{-5+1}{2\cdot (-1)}=2$

Stąd wynika, że $\dpi{120} x\in (2;3).$

Pokaż rozwiązanie

Zwiń

e) $\dpi{120} \begin{vmatrix} x & 1 &1 \\ 1& x &1 \\ 1 &1 &x \end{vmatrix}> 0,$

Rozwiązanie

Liczymy wyznacznik:

$\dpi{120} \begin{vmatrix} x & 1 &1 \\ 1 &x & 1\\ 1&1 & x \end{vmatrix}\begin{matrix} x & 1\\ 1 &x \\ 1& 1 \end{matrix}=$

$\dpi{120} =x\cdot x\cdot x+1\cdot 1\cdot 1+1\cdot 1\cdot 1-1\cdot 1\cdot x-x\cdot 1\cdot 1-1\cdot x\cdot 1=$

$\dpi{120} =x^{3}+1+1-x-x-x=$

$\dpi{120} =x^{3}-3x+2$

Wracamy do nierówności:

$\dpi{120} x^{3}-3x+2> 0$

Zauważmy, że liczba 1 jest pierwiastkiem wielomianu $\dpi{120} {\color{Red} 1}x^{3}+{\color{Green} 0}x^{2}{\color{Blue} -3}x+{\color{Yellow} 2},$ wobec tego wielomian ten dzieli się przez $\dpi{120} x-{\color{Magenta} 1}$ . Wykorzystamy schemat Hornera dla $\dpi{120} c={\color{Magenta} 1}$ . Dokładny opis schematu Hornera tutaj

1	0	-3	2
1	1·1+0=1	1·1+(-3)=-2	-2·1+2=0

Mamy zatem, że $\dpi{120} (x^{3}-3x+2):(x-1)={\color{Red} 1}x^{2}+{\color{DarkGreen} 1}x{\color{DarkRed} -2}.$ Szukamy miejsc zerowych $\dpi{120} x^{2}+x-2.$

$\dpi{120} \Delta =1-4\cdot 1\cdot (-2)=1+8=9,\; \sqrt{\Delta }=3$

$\dpi{120} x_{1}=\frac{-1-3}{2\cdot 1}=-2,\; x_{2}=\frac{-1+3}{2\cdot 1}=1$

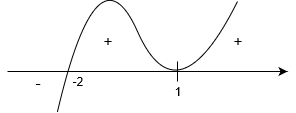
Otrzymaliśmy zatem, że $\dpi{120} x^{3}-3x+2=(x-1)^{2}(x+2).$ Wracając do nierówności:

$\dpi{120} (x-1)^{2}(x+2)> 0\Rightarrow x\in (-2;+\infty )-\left \{ 1 \right \}.$

Pokaż rozwiązanie

Zwiń

f) $\dpi{120} \begin{vmatrix} 1+i & 1 & x\\ 1 &0 &1-i \\ x & 1-i & 1 \end{vmatrix}=3+2i.$

Rozwiązanie

W zadaniu tym zostały połączone wiadomości z liczb zespolonych oraz z wyznaczników. Liczymy wyznacznik:

$\dpi{120} \begin{vmatrix} 1+i & 1 &x \\ 1& 0 &1-i \\ x & 1-i & 1 \end{vmatrix}\begin{matrix} 1+i & 1\\ 1&0 \\ x &1-i \end{matrix}=$

$\dpi{120} =(1+i)\cdot 0\cdot 1+1\cdot (1-i)\cdot x+x\cdot 1\cdot (1-i)-1\cdot 1\cdot 1-(1+i)\cdot (1-i)(1-i)-x\cdot 0\cdot x=$

$\dpi{120} =0+x-ix+x-ix-1-(1-i^{2})(1-i)-0=$

$\dpi{120} =2x-2ix-1-\overset{=2}{\overbrace{(1+1)}}(1-i)=$

$\dpi{120} =2x-2ix-1-2+2i=$

$\dpi{120} =x(2-2i)-3+2i$

Wracamy do równania:

$\dpi{120} x(2-2i)-3+2i=3+2i$

$\dpi{120} x(2-2i)=3+2i+3-2i$

$\dpi{120} x(2-2i)=6/:(2-2i)$

$\dpi{120} x=\frac{6}{2-2i}$

$\dpi{120} x=\frac{6}{2(1-i)}$

$\dpi{120} x=\frac{3}{1-i}\cdot \frac{1+i}{1+i}$ (mnożymy licznik i mianownik przez sprzężenie mianownika)

$\dpi{120} x=\frac{3+3i}{1-i^{2}}=\frac{3+3i}{1+1}=\frac{3+3i}{2}=\frac{3}{2}(1+i).$

Pokaż rozwiązanie

Zwiń

Zadanie 3. Stosując rozwinięcie Laplace’a obliczyć wyznaczniki:

Proszę wykonać podpunkty po kolei. W podpunktach a) i b) rozwiązania są bardzo dokładne, w c) i d) trochę mniej. W podpunkcie e) wkracza nowa wiedza, więc nie można go pominąć. Kolejne podpunkty utrwalają wiedzę.

a) $\dpi{120} \begin{vmatrix} 1 & -1 &0 & 2\\ 2 & 1 & -3 &1 \\ 3 & 0 & 0 &-2 \\ -1 &2 &0 &2 \end{vmatrix}$ ,

Rozwiązanie

Aby zastosować rozwinięcie Laplace’a należy wybrać dowolny wiersz (lub kolumnę), względem którego będziemy go stosować. Może to być każdy z nich, nie ma żadnych ograniczeń. Ze względów rachunkowych radzimy wybierać ten wiersz (lub kolumnę), w którym mamy jak najwięcej zer. W naszym przypadku najlepiej wybrać trzecią kolumnę (3 zera). Zatem stosujemy rozwinięcie Laplace’a względem trzeciej kolumny:

$\dpi{120} \begin{vmatrix} 1 &-1 &{\color{Red} 0} & 2\\ 2& 1 &{\color{Green} -3} &1 \\ 3 & 0 &{\color{Blue} 0 }&-2 \\ -1 & 2 &{\color{Magenta} 0} &2 \end{vmatrix}\overset{1.}{=}$

$\dpi{120} \overset{1.}{=}\overset{0}{\overbrace{{\color{Red} 0}\cdot (-1)^{1+3}\begin{vmatrix} 2 & 1 &1 \\ 3 &0 &-2 \\ -1&2 & 2 \end{vmatrix}}}+({\color{Green} -3})\cdot (-1)^{2+3}\begin{vmatrix} 1 &-1 &2 \\ 3& 0 & -2\\ -1 &2 & 2 \end{vmatrix}+\overset{0}{\overbrace{{\color{Blue} 0}\cdot (-1)^{3+3}\begin{vmatrix} 1 & -1 & 2\\ 2& 1 & 1\\ -1&2 & 2 \end{vmatrix}}}+$

$\dpi{120} +\overset{0}{\overbrace{{\color{Magenta} 0}\cdot (-1)^{4+3}\begin{vmatrix} 1 & -1 & 2\\ 2 &1 &1 \\ 3 & 0 &-2 \end{vmatrix}}}=$

1. W trzeciej kolumnie mamy kolejno elementy 0,-3 0, 0. Stąd w rozwinięciu Laplace’a cztery składniki sumy odpowiadające tym elementom. Każdy składnik jest iloczynem trzech czynników:

elementu z wybranej u nas kolumny (ew. wiersza), np. -3 to drugi element kolumny, patrzmy na drugi składnik sumy
$\dpi{120} (-1)^{m+n}$ , gdzie $\dpi{120} m$ i $\dpi{120} n$ są wskaźnikami mówiącymi na przecięciu, którego wiersza i kolumny leży dany element macierzy np. -3 leży na przecięciu 2 wiersza i 3 kolumny, stąd $\dpi{120} (-1)^{2+3}$
wyznacznika macierzy powstałej przez wykreślenie odpowiedniego wiersza i kolumny z wyjściowej macierzy. Wskaźniki $\dpi{120} m$ i $\dpi{120} n$ z poprzedniego podpunktu mówią nam, który wiersz i którą kolumnę wykreślamy. W przypadku elementu -3 skreślamy wiersz 2 i kolumnę 3. Nie pomylić kolejności: wiersz, kolumna. Powstaje nam wówczas wyznacznik $\begin{vmatrix} 1 & -1 & 2\\ 3&0 &-2 \\ -1 &2 &2 \end{vmatrix}$ .

Tak postępujemy z każdym elementem w wybranej kolumnie. U nas są to same zera. Widzimy teraz, dlaczego opłaca się wybierać wiersze (kolumny) z duża ilością zer. W poszczególnych składnikach sumy mamy wówczas mnożenie przez zero, więc te składniki się zerują. W naszym przypadku są to składniki pierwszy, trzeci i czwarty.

Nie przechodzić dalej, dopóki nie zrozumiecie tego kroku!

Zatem nasz wyznacznik (po uwzględnieni zer) jest równy:

$\dpi{120} \begin{vmatrix} {\color{Blue} 1} & {\color{Blue} -1} & 0 &{\color{Blue} 2}\\ 2 &1 & {\color{Red} -3} &1 \\ {\color{Blue} 3} &{\color{Blue} 0} & 0 & {\color{Blue} -2}\\ {\color{Blue} -1} &{\color{Blue} 2} & 0&{\color{Blue} 2} \end{vmatrix}=({\color{Red} -3})\cdot \overset{-1}{\overbrace{(-1)^{2+3}}}\begin{vmatrix} {\color{Blue} 1 }&{\color{Blue} -1} &{\color{Blue} 2} \\ {\color{Blue} 3}&{\color{Blue} 0} & {\color{Blue} -2}\\ {\color{Blue} -1} &{\color{Blue} 2 }&{\color{Blue} 2} \end{vmatrix}\overset{2.}{=}$

$\dpi{120} \overset{2.}{=}\overset{3}{\overbrace{(-3)\cdot (-1)}}\cdot \begin{vmatrix} 1 & -1 &2 \\ 3 & 0 &-2 \\ -1 &2 &2 \end{vmatrix}\begin{matrix} 1 & -1\\ 3 &0 \\ -1 &2 \end{matrix}=$

2. Uwzględniliśmy, że $(-1)^{2+3}=-1.$ Przystępujemy do liczenia wyznacznika trzeciego stopnia metodą Sarrusa poznaną w poprzednim zadaniu. Dopisaliśmy zatem dwie kolumny za macierzą, aby teraz tworzyć odpowiednie przekątne.

$\dpi{120} =3\cdot \left [ 1\cdot 0\cdot 2+(-1)\cdot (-2) \cdot (-1)+2\cdot 3\cdot 2-(-1)\cdot 3\cdot 2-1\cdot (-2)\cdot 2-2\cdot 0\cdot (-1)\right ]=$

$\dpi{120} =3\cdot (0-2+12+6+4+0)=3\cdot 20=60.$

Pokaż rozwiązanie

Zwiń

b) $\dpi{120} \begin{vmatrix} 1 & 0 &4 &0 \\ 3 &2 & 0 & 1\\ -2 & -1 & 0 & 2\\ 1 &-1 &1 & 4 \end{vmatrix}$ ,

Rozwiązanie

W tym przypadku możemy wybrać np. pierwszy wiersz (2 zera) lub trzecią kolumnę (2 zera). Wybierzmy zatem trzecią kolumnę. Zatem rozwinięcie Laplace’a ma postać:

$\dpi{120} \begin{vmatrix} 1 & 0 &{\color{Red} 4} &0 \\ 3 &2 & {\color{Green} 0} & 1\\ -2 & -1 & {\color{Blue} 0} &2 \\ 1 & -1 &{\color{Magenta} 1} & 4 \end{vmatrix}\overset{1.}{=}$

$\dpi{120} \overset{1.}{=}{\color{Red} 4}\cdot (-1)^{1+3}\begin{vmatrix} 3 & 2 & 1\\ -2&-1 &2 \\ 1 & -1 & 4 \end{vmatrix}{\underset{0}{\underbrace{+{\color{Green} 0}\cdot (-1)^{2+3}\begin{vmatrix} 1 & 0 & 0\\ -2 & -1 &2 \\ 1 & -1 & 4 \end{vmatrix}}}}+\underset{0}{\underbrace{{\color{Blue} 0}\cdot (-1)^{3+3}\begin{vmatrix} 1 & 0 &0 \\ 3 & 2 & 1\\ 1 &-1 & 4 \end{vmatrix}}}+$

$\dpi{120} +{\color{Magenta} 1}\cdot (-1)^{4+3}\begin{vmatrix} 1 & 0 & 0\\ 3 & 2 & 1\\ -2&-1 & 2 \end{vmatrix}=$

1. W trzeciej kolumnie mamy kolejno elementy 4, 0, 0, 1. Stąd w rozwinięciu Laplace’a cztery składniki sumy odpowiadające tym elementom. Każdy składnik jest iloczynem trzech czynników:

elementu z wybranej u nas kolumny (ew. wiersza), np. 4
$(-1)^{m+n},$ gdzie $m$ i $n$ są wskaźnikami mówiącymi na przecięciu, którego wiersza i kolumny leży dany element macierzy np. 4 leży na przecięciu 1 wiersza i 3 kolumny, stąd $(-1)^{1+3}$
wyznacznika macierzy powstałej przez wykreślenie odpowiedniego wiersza i kolumny z wyjściowej macierzy. Wskaźnik $m$ i $n$ z poprzedniego podpunktu mówią nam, który wiersz i którą kolumnę wykreślamy. W przypadku elementu 4 skreślamy wiersz 1 i kolumnę 3. Nie pomylić kolejności: wiersz, kolumna. Powstaje nam wówczas wyznacznik $\begin{vmatrix} 3 &2 &1 \\ -2& -1 &2 \\ 1& -1 &4 \end{vmatrix}$ .

Tak postępujemy z każdym elementem w wybranej kolumnie. W poszczególnych składnikach sumy mamy wówczas mnożenie przez zero, więc te składniki się zerują. W naszym przypadku są to składniki drugi i trzeci.

Zatem nasz wyznacznik (po uwzględnieniu zer) jest równy:

$\dpi{120} \begin{vmatrix} 1 & 0 &4 & 0\\ 3 &2 &0 & 1\\ -2&-1 & 0 & 2\\ 1 & -1 & 1 &4 \end{vmatrix}=\overset{=4}{\overbrace{4\cdot (-1)^{1+3}}}\begin{vmatrix} 3 &2 & 1\\ -2& -1 &2 \\ 1 &-1 & 4 \end{vmatrix}+\overset{=-1}{\overbrace{1\cdot (-1)^{4+3}}}\begin{vmatrix} 1 & 0 &0 \\ 3 & 2 & 1\\ -2 &-1 & 2 \end{vmatrix}\overset{2.}{=}$

$\dpi{120} \overset{2.}{=}4\cdot \begin{vmatrix} 3 & 2 &1 \\ -2& -1 &2 \\ 1 &-1 & 4 \end{vmatrix}\begin{matrix} 3 &2 \\ -2 &-1 \\ 1 &-1 \end{matrix}+\left (-1 \right )\cdot \begin{vmatrix} 1 & 0 &0 \\ 3&2 & 1\\ -2&-1 & 2 \end{vmatrix}\begin{matrix} 1 &0 \\ 3 &2 \\ -2& -1 \end{matrix}=$

2. Uwzględniliśmy, że $(-1)^{1+3}=1$ oraz $(-1)^{4+3}=-1.$ Przystępujemy do liczenia wyznacznika trzeciego stopnia metodą Sarrusa poznaną wcześniej. Dopisaliśmy zatem po dwie kolumny za macierzami, aby teraz tworzyć odpowiednie przekątne.

$\dpi{120} =4\cdot \left [ 3\cdot (-1) \cdot 4+2\cdot 2\cdot 1+1\cdot (-2)\cdot (-1)-2\cdot\left ( -2 \right )\cdot 4-3\cdot 2\cdot (-1)-1\cdot (-1)\cdot 1\right ]-$

$\dpi{120} -1\cdot \left [ 1\cdot 2\cdot 2+0\cdot 1\cdot (-2)+0\cdot 3\cdot (-1)-0\cdot 3\cdot 2-1\cdot 1\cdot (-1) -0\cdot 2\cdot (-2)\right ]=$

$\dpi{120} =4(-12+4+2+16+6+1)-1(4+0+0+0+1+0)=4\cdot 17-1\cdot 5=68-5=63.$

Pokaż rozwiązanie

Zwiń

c) $\dpi{120} \begin{vmatrix} 1 &3 & 4 & 5\\ 3& 0 &0 & 2\\ 5&1 &2 & 7\\ 2 & 0 & 0 & 3 \end{vmatrix}$ ,

Rozwiązanie

Tym razem możemy wybrać do rozwinięcia Laplace’a np. drugą kolumnę lub drugi wiersz, trzecią kolumnę lub trzeci wiersz. Wszędzie mamy dwa zera. Wybierzmy zatem drugi wiersz. Mamy:

$\dpi{120} \begin{vmatrix} 1 &3 & 4 & 5\\ {\color{Red} 3}& {\color{Green} 0} &{\color{Blue} 0} & {\color{Magenta} 2}\\ 5&1 &2 & 7\\ 2 & 0 & 0 & 3 \end{vmatrix}=$

$\dpi{120} ={\color{Red} 3}\cdot (-1)^{2+1}\begin{vmatrix} 3 &4 &5 \\ 1& 2 &7 \\ 0 & 0 & 3 \end{vmatrix}+\overset{=0}{\overbrace{{\color{Green} 0}\cdot (-1)^{2+2}\begin{vmatrix} 1 & 4 &5 \\ 5& 2 &7 \\ 2 & 0 & 3 \end{vmatrix}}}+\overset{=0}{\overbrace{{\color{Blue} 0}\cdot (-1)^{2+3}\begin{vmatrix} 1 & 3 &5 \\ 5 & 1 &7 \\ 2& 0 & 3 \end{vmatrix}}}+$

$\dpi{120} +{\color{Magenta} 2}\cdot (-1)^{2+4}\begin{vmatrix} 1 & 3 & 4\\ 5 &1 &2 \\ 2 & 0 & 0 \end{vmatrix}=$

$\dpi{120} =3\cdot (-1)\begin{vmatrix} 3 & 4 &5 \\ 1 & 2 & 7\\ 0&0 & 3 \end{vmatrix}\begin{matrix} 3 &4 \\ 1&2 \\ 0& 0 \end{matrix}+2\cdot \begin{vmatrix} 1 & 3 &4 \\ 5 & 1 &2 \\ 2& 0& 0 \end{vmatrix}\begin{matrix} 1 &3 \\ 5& 1\\ 2& 0 \end{matrix}=$

$\dpi{120} =-3\cdot (3\cdot 2\cdot 3+4\cdot 7\cdot 0+5\cdot 1\cdot 0-4\cdot 1\cdot 3-3\cdot 7\cdot 0-5\cdot 2\cdot 0)+$

$\dpi{120} +2\cdot (1\cdot 1\cdot 0+3\cdot 2\cdot 2+4\cdot 5\cdot 0-3\cdot 5\cdot 0-1\cdot 2\cdot 0-4\cdot 1\cdot 2)=$

$\dpi{120} =-3\cdot (18+0+0-12-0-0)+2\cdot (0+12+0-0-0-8)=-3\cdot 6+2\cdot 4=-10.$

Gdyby nie wszystko było zrozumiałe zalecamy wrócić do podpunktów a) i b), gdzie tłumaczenia są dużo dokładniejsze.

Pokaż rozwiązanie

Zwiń

d) $\dpi{120} \begin{vmatrix} -3 & -1 & 2 & 1\\ 2 & 0 & -2 &-1 \\ 4& 0 & -3 & 2\\ -4& 3 & 0 & -2 \end{vmatrix}$ ,

Rozwiązanie

Zastosujmy rozwinięcie Laplece’a do drugiej kolumny, gdyż tam jest najwięcej zer. Otrzymujemy:

$\dpi{120} \begin{vmatrix} -3 & {\color{Red} -1} & 2 & 1\\ 2 & {\color{Green} 0} & -2 &-1 \\ 4& {\color{Blue} 0} & -3 & 2\\ -4& {\color{Magenta} 3 }& 0 & -2 \end{vmatrix}=$

$\dpi{120} ={\color{Red} -1}\cdot (-1)^{1+2}\begin{vmatrix} 2 & -2 &-1 \\ 4 &-3 &2 \\ -4&0 & -2 \end{vmatrix}+\overset{0}{\overbrace{{\color{Green} 0}\cdot (-1)^{2+2}\begin{vmatrix} -3 &2 & 1\\ 4 &-3 &2 \\ -4 & 0 & -2 \end{vmatrix}}}+\overset{0}{\overbrace{{\color{Blue} 0}\cdot (-1)^{3+2}\begin{vmatrix} -3 & 2 &1 \\ 2&-2 &-1 \\ -4& 0& -2 \end{vmatrix}}}+$

$\dpi{120} +{\color{Magenta} 3}\cdot (-1)^{4+2}\begin{vmatrix} -3 & 2 &1 \\ 2&-2 & -1\\ 4& -3 & 2 \end{vmatrix}=$

$\dpi{120} =-1\cdot (-1)\begin{vmatrix} 2 & -2 & -1\\ 4 & -3& 2\\ -4&0 & -2 \end{vmatrix}\begin{matrix} 2 & -2\\ 4 &-3 \\ -4 &0 \end{matrix}+3\cdot \begin{vmatrix} -3 & 2 &1 \\ 2 & -2 & -1\\ 4 &-3 &2 \end{vmatrix}\begin{matrix} -3 & 2\\ 2& -2\\ 4 &-3 \end{matrix}=$

$\dpi{120} =1\cdot \left [ 2\cdot (-3) \cdot (-2)+ \left ( -2 \right )\cdot 2\cdot (-4)+(-1)\cdot 4\cdot 0-(-2)\cdot 4\cdot (-2)-2\cdot 2\cdot 0-(-1)\cdot (-3)\cdot (-4)\right ]+$

$\dpi{120} +3\cdot \left [ (-3)\cdot (-2)\cdot 2+2\cdot (-1) \cdot 4+1\cdot 2\cdot (-3)-2\cdot 2\cdot 2-(-3)\cdot (-1)\cdot (-3)-1\cdot (-2)\cdot 4\right ]=$

$\dpi{120} =(12+16+0-16-0+12)+3\cdot (12-8-6-8+9+8)=24+3\cdot 7=45.$

Gdyby nie wszystko było zrozumiałe zalecamy wrócić do podpunktów a) i b), gdzie tłumaczenia są dużo dokładniejsze.

Pokaż rozwiązanie

Zwiń

e) $\dpi{120} \begin{vmatrix} 1 & 1 &-1 & 1\\ 2& -1 & 1 & 1\\ 1& 2 & 3 &-1 \\ 3 & -1 & 2 & -1 \end{vmatrix}$ ,

Rozwiązanie

Jak widzimy w macierzy nie ma żadnego zera. Można stosować oczywiście od razu rozwinięcie Laplace’a, ale będzie do policzenia cztery wyznaczniki trzeciego stopnia. A jeżeli spojrzymy do ostatnich podpunktów tego zadania, byłoby tam cztery bądź aż pięć wyznaczników stopnia czwartego, do których znowu trzeba stosować rozwinięcie Laplace’a. Zbyt długo. Dlatego wygodne jest tzw. tworzenie dodatkowych zer w macierzy. Stosuje się do tego przekształcenia elementarne (patrz zakładka teoria). Najpierw wybierzmy wiersz (lub kolumnę), w której utworzymy zera. Ze względów rachunkowych najwygodniej jest wybrać wiersz (kolumnę), w której mamy liczbę 1 lub -1. Aby wyraźniej były widoczne operacje jakie będziemy wykonywać zdecydujmy się na pierwszą kolumnę.

tworzymy zero na pozycji $\dpi{120} a_{21}$ , czyli w miejscu liczby 2. Wychodzimy od liczby 1 stojącej na pozycji $\dpi{120} a_{11}$ . Aby wyzerować liczbę 2 liczbę 1 należy pomnożyć przez -2 i dodać do wspomnianej liczby 2. Operację tę musimy przeprowadzić na całych wierszach, które zawierają te liczby. Czyli pierwszy wiersz mnożymy przez -2 i dodajemy do wiersza drugiego. Ogólna zasada: jeżeli wybraliśmy kolumnę, w której tworzymy zera, wszelkie operacje wykonujemy na wierszach. Jeżeli wybraliśmy wiersz, to operacje wykonujemy na kolumnach. Otrzymujemy:

$\dpi{120} \begin{vmatrix}{\color{Red} 1} & {\color{Red} 1} & {\color{Red} -1} &{\color{Red} 1 }\\ {\color{Blue} 2}& {\color{Blue} -1} & {\color{Blue} 1} &{\color{Blue} 1} \\ 1& 2 & 3& -1\\ 3 & -1 &2 &-1 \end{vmatrix}\overset{Iw\cdot ( {\color{Purple} -2})+IIw}{=}$

$\dpi{120} \overset{Iw\cdot ( {\color{Purple} -2})+IIw}{=}\begin{vmatrix} {\color{Red} 1} &{\color{Red} 1} & {\color{Red} -1} &{\color{Red} 1 }\\ {\color{Blue} 2}+({\color{Purple} -2})\cdot {\color{Red} 1}&{\color{Blue} -1}+({\color{Purple} -2}) \cdot{\color{Red} 1} & {\color{Blue} 1}+({\color{Purple} -2})\cdot ({\color{Red} -1}) &{\color{Blue} 1}+({\color{Purple} -2})\cdot {\color{Red} 1} \\ 1& 2 & 3 & -1\\ 3 & -1 &2 & -1 \end{vmatrix}=$

$\dpi{120} =\begin{vmatrix} 1 & 1 & -1 & 1\\ 0& -3 & 3 &-1 \\ {\color{Red} 1} & 2 &3 & -1\\ 3 & -1 & 2 & -1 \end{vmatrix}$

tworzymy zero na pozycji $\dpi{120} a_{31}$ , czyli w miejscu liczby 1. Podobnie jak poprzednio wychodzimy od liczby 1 z pozycji $\dpi{120} a_{11}$ i mnożymy ją przez -1, następnie dodajemy do -1 z $\dpi{120} a_{31}$ . Operacje wykonujemy na całych wierszach. Zatem:

$\dpi{120} \begin{vmatrix} {\color{Red} 1} & {\color{Red} 1} & {\color{Red} -1} & {\color{Red} 1}\\ 0&-3 & 3 &-1 \\ {\color{Blue} 1} &{\color{Blue} 2} &{\color{Blue} 3} & {\color{Blue} -1}\\ 3 &-1 & 2 & -1 \end{vmatrix}\overset{Iw\cdot ({\color{Purple} -1})+IIIw}{=}$

$\dpi{120} \overset{Iw\cdot ({\color{Purple} -1})+IIIw}{=}\begin{vmatrix} 1 & 1 & -1 & 1\\ 0& -3& 3 & -1\\ {\color{Blue} 1}+({\color{Purple} -1})\cdot {\color{Red} 1}& {\color{Blue} 2}+({\color{Purple} -1})\cdot {\color{Red} 1} & {\color{Blue} 3}+({\color{Purple} -1}) \cdot ({\color{Red} -1})& {\color{Blue} -1}+({\color{Purple} -1})\cdot {\color{Red} 1}\\ 3& -1 &2 & -1 \end{vmatrix}=$

$\dpi{120} =\begin{vmatrix} 1 & 1 & -1 &1 \\ 0 & -3 & 3 &-1 \\ 0& 1 & 4 &-2 \\ {\color{Red} 3} &-1 & 2 & -1 \end{vmatrix}$

tworzymy zero na pozycji $\dpi{120} a_{41}$ , czyli w miejscu liczby 3. Podobnie jak poprzednio wychodzimy od liczby 1 z pozycji $\dpi{120} a_{11}$ i mnożymy ją przez -3, następnie dodajemy do 3 z $\dpi{120} a_{41}$ . Operację wykonujemy na całych wierszach. Zatem:

$\dpi{120} \begin{vmatrix} {\color{Red} 1} & {\color{Red} 1} & {\color{Red} -1} &{\color{Red} 1} \\ 0 & -3 & 3 &-1 \\ 0 & 1 & 4 &-2 \\ {\color{Blue} 3}& {\color{Blue} -1} &{\color{Blue} 2} & {\color{Blue} -1} \end{vmatrix}\overset{Iw\cdot ({\color{Purple} -3})+IVw}{=}$

$\dpi{120} \overset{Iw\cdot ({\color{Purple} -3})+IVw}{=}\begin{vmatrix} 1 & 1 &-1 & 1\\ 0 & -3& 3 &-1 \\ 0& 1 &4 &-2 \\ {\color{Blue} 3}+({\color{Purple} -3})\cdot {\color{Red} 1} & {\color{Blue} -1}+({\color{Purple} -3})\cdot {\color{Red} 1} & {\color{Blue} 2}+({\color{Purple} -3})\cdot ({\color{Red} -1}) & {\color{Blue} -1}+({\color{Purple} -3})\cdot {\color{Red} 1} \end{vmatrix}=$

$\dpi{120} =\begin{vmatrix} 1 & 1 & -1 &1 \\ 0 & -3 &3 &-1 \\ 0 & 1 & 4 &-2 \\ 0 &-4 & 5 & -4 \end{vmatrix}$

W pierwszej kolumnie otrzymaliśmy trzy zera i właśnie do niej zastosujemy rozwinięcie Laplace’a. Pominiemy już składniki w rozwinięciu Laplace’a, które się zerują. Mamy więc:

$\dpi{120} \begin{vmatrix} {\color{Red} 1} & 1 &-1 & 1\\ 0 & {\color{Blue} -3} &{\color{Blue} 3} & {\color{Blue} -1}\\ 0& {\color{Blue} 1} & {\color{Blue} 4}& {\color{Blue} -2}\\ 0 & {\color{Blue} -4} &{\color{Blue} 5 }& {\color{Blue} -4} \end{vmatrix}=\overset{1}{\overbrace{{\color{Red} 1}\cdot (-1)^{1+1}}}\begin{vmatrix}{\color{Blue} -3} &{\color{Blue} 3} & {\color{Blue} -1}\\ {\color{Blue} 1} & {\color{Blue} 4} &{\color{Blue} -2} \\ {\color{Blue} -4} &{\color{Blue} 5} & {\color{Blue} -4} \end{vmatrix}\begin{matrix} -3 &3 \\ 1&4 \\ -4 & 5 \end{matrix}=$

$\dpi{120} =-3\cdot 4\cdot (-4)+3\cdot (-2)\cdot (-4)+(-1)\cdot 1\cdot 5-$

$\dpi{120} -3\cdot 1\cdot (-4)-(-3)\cdot (-2)\cdot 5-(-1)\cdot 4\cdot (-4)=$

$\dpi{120} =48+24-5+12-30-16=33.$

Pokaż rozwiązanie

Zwiń

f) $\dpi{120} \begin{vmatrix} 2 & -1 & 1&3 \\ -3 & 3 & 1 & 2\\ 1& 2 &-2 & 1\\ 4& -4 & 1 &1 \end{vmatrix}$ ,

Rozwiązanie

Wybierzmy wiersz lub kolumnę, w której będziemy tworzyli zera. Ponieważ w poprzednim przykładzie wybraliśmy kolumnę, więc teraz dla odmiany wybierzmy drugi wiersz. Pamiętajmy, wybór wiersza czy kolumny jest zupełnie dowolny. Na pozycji $\dpi{120} a_{23}$ mamy liczbę 1, która będzie naszym punktem wyjścia. Ponieważ wybraliśmy wiersz wszystkie operacje będziemy przeprowadzali na kolumnach. Zatem trzecią kolumnę mnożymy przez 3 i dodajemy do pierwszej kolumny. Dostaniemy zero na pozycji $\dpi{120} a_{21}$ (w miejscu liczby -3)

$\dpi{120} \begin{vmatrix} 2 &-1 & 1 &3 \\ -3& 3 & 1 & 2\\ 1 & 2 & -2 &1 \\ 4 & -4 & 1 & 1 \end{vmatrix}\overset{IIIk\cdot 3+Ik}{=}\begin{vmatrix} 2+3\cdot 1 & -1 &1 &3 \\ -3+3\cdot 1 & 3 & 1 & 2\\ 1+3\cdot (-2)&2 & -2 &1 \\ 4+3\cdot 1 & -4 &1 & 1 \end{vmatrix}=\begin{vmatrix} 5 &-1 &1 &3 \\ 0& 3 & 1 & 2\\ -5& 2 &-2 &1 \\ 7 & -4 &1 & 1 \end{vmatrix}=$

Kolejne zero tworzymy na pozycji $\dpi{120} a_{22}$ . Mnożymy kolumnę trzecią przez -3 i dodajemy do kolumny drugiej.

$\dpi{120} =\begin{vmatrix} 5 & -1 &1 &3 \\ 0 & 3 &1 &2 \\ -5 & 2 & -2 &1 \\ 7& -4&1 & 1 \end{vmatrix}\overset{IIIk\cdot (-3)+IIk}{=}\begin{vmatrix} 5 & -1+(-3) \cdot 1& 1&3 \\ 0& 3+(-3)\cdot 1 &1 &2 \\ -5& 2+(-3)\cdot (-2) &-2 &1 \\ 7 & -4+(-3) \cdot 1&1 & 1 \end{vmatrix}=\begin{vmatrix} 5 & -4 & 1 & 3\\ 0 & 0 & 1 &2 \\ -5&8 & -2 &1 \\ 7 &-7 & 1 & 1 \end{vmatrix}=$

Teraz pomnóżmy trzecią kolumnę przez -2 i dodajmy do czwartej kolumny. Otrzymamy zero na pozycji $\dpi{120} a_{24}.$

$\dpi{120} =\begin{vmatrix} {\color{Blue} 5} & {\color{Blue} -4} & 1 & {\color{Blue} 1}\\ 0&0 &{\color{Red} 1 }& 0\\ {\color{Blue} -5} &{\color{Blue} 8} &-2 & {\color{Blue} 5}\\ {\color{Blue} 7} & {\color{Blue} -7} & 1 & {\color{Blue} -1 }\end{vmatrix}=\overset{-1}{\overbrace{{\color{Red} 1}\cdot (-1)^{2+3}}}\begin{vmatrix} {\color{Blue} 5} & {\color{Blue} -4} &{\color{Blue} 1} \\ {\color{Blue} -5} & {\color{Blue} 8} &{\color{Blue} 5}\\ {\color{Blue} 7} & {\color{Blue} -7} &{\color{Blue} -1} \end{vmatrix}=-1\cdot \begin{vmatrix} 5 &-4 &1 \\ -5& 8 & 5\\ 7 & -7& -1 \end{vmatrix}$

Można liczyć ten wyznacznik metodą Sarrusa. My pokażemy, że rozwinięcie Laplace’a można stosować stosować również do wyznaczników trzeciego stopnia. Najpierw jednak utwórzmy w tym więcej zer. Pamiętajmy, nie są to koniecznie przekształcenia.

$\dpi{120} -1\cdot \begin{vmatrix} 5 &-4 &1 \\ -5 &8 & 5\\ 7& -7 & -1 \end{vmatrix}\overset{IIk+Ik}{=}-1\cdot \begin{vmatrix} 5+(-4) &-4 &1 \\ -5+8 & 8 &5 \\ 7+(-7)& -7 &-1 \end{vmatrix}=$

$\dpi{120} =-1\cdot \begin{vmatrix} 1 &-4 & 1\\ 3 & 8 & 5\\ 0&-7 & -1 \end{vmatrix}\overset{IIIk\cdot (-7)+IIk}{=}$

$\dpi{120} =-1\cdot \begin{vmatrix} 1 &-4+(-7)\cdot 1 &1 \\ 3&8+(-7)\cdot 5 &5 \\ 0&-7+(-7)\cdot (-1) & -1 \end{vmatrix}=-1\cdot \begin{vmatrix} 1 & -11 &1 \\ 3&-27 &5 \\ 0 & 0 &-1 \end{vmatrix}=$

Stosujemy rozwinięcie Laplace’a względem trzeciego wiersza:

$\dpi{120} ={\color{Red} -1}\cdot \begin{vmatrix} {\color{Blue} 1} &{\color{Blue} -11} &1 \\ {\color{Blue} 3} &{\color{Blue} -27} & 5\\ 0& 0 & {\color{Green} -1} \end{vmatrix}=\overset{1}{\overbrace{{\color{Red} -1}\cdot ({\color{Green} -1})\cdot (-1)^{3+3}}}\begin{vmatrix} {\color{Blue} 1} &{\color{Blue} -11} \\ {\color{Blue} 3 }& {\color{Blue} -27 }\end{vmatrix}=$

$\dpi{120} =1\cdot (-27)-(-11)\cdot 3=-27+33=6$

Pokaż rozwiązanie

Zwiń

g) $\dpi{120} \begin{vmatrix} 2 & 1 & 0 &6 \\ 3& -1 & 7 & 4\\ 1& 0 &1 &2 \\ -1 & -2 & 1 & 5 \end{vmatrix}$ ,

Rozwiązanie

Wybierzmy do tworzenia zer trzeci wiersz.

$\dpi{120} \begin{vmatrix} 2 & 1 & 0 &6 \\ 3& -1 & 7 & 4\\ 1& 0 &1 &2 \\ -1 & -2 & 1 & 5 \end{vmatrix}\overset{Ik\cdot \left ( -1 \right )+IIIk}{=}\begin{vmatrix} 2 & 1 & 0+\left ( -1 \right )\cdot 2& 6\\ 3 & -1 & 7+\left ( -1 \right ) \cdot 3&4 \\ 1& 0& 1+\left ( -1 \right )\cdot 1 & 2\\ -1 & -2& 1+\left ( -1 \right )\cdot \left ( -1 \right ) & 5 \end{vmatrix}=$

$\dpi{120} =\begin{vmatrix} 2 & 1& -2& 6\\ 3 &-1 & 4& 4\\ 1& 0 & 0& 2\\ -1& -2& 2& 5 \end{vmatrix}\overset{Ik\cdot \left ( -2 \right )+IVk}{}=\begin{vmatrix} 2 & 1& -2& 6+\left ( -2 \right )\cdot 2\\ 3& -1& 4& 4+\left ( -2 \right )\cdot 3\\ 1& 0& 0& 2+\left ( -2 \right )\cdot 1\\ -1& -2& 2& 5+\left ( -2 \right )\cdot \left ( -1 \right ) \end{vmatrix}=$

$\dpi{120} =\begin{vmatrix} 2 & 1 & -2& 2\\ 3& -1 & 4 & -2\\ 1 & 0 & 0& 0\\ -1 & -2 & 2 & 7 \end{vmatrix}=$

Stosujemy rozwinięcie Laplace’a względem trzeciego wiersza:

$\dpi{120} =\begin{vmatrix} 2 & {\color{Blue} 1}& {\color{Blue} -2} &{\color{Blue} 2} \\ 3& {\color{Blue} -1} & {\color{Blue} 4} & {\color{Blue} -2}\\ {\color{Red} 1} & 0& 0& 0\\ -1& {\color{Blue} -2} &{\color{Blue} 2} &{\color{Blue} 7} \end{vmatrix}=\overset{1}{\overbrace{{\color{Red} 1}\cdot \left ( -1 \right )^{3+1}}}\begin{vmatrix} {\color{Blue} 1} & {\color{Blue} -2} &{\color{Blue} 2} \\ {\color{Blue} -1}& {\color{Blue} 4}& {\color{Blue} -2}\\ {\color{Blue} -2}&{\color{Blue} 2} & {\color{Blue} 7 }\end{vmatrix}=$

$\dpi{120} =\begin{vmatrix} 1 &-2 &2 \\ -1& 4 & -2\\ -2 & 2 & 7 \end{vmatrix}=$

Można liczyć ten wyznacznik metodą Sarrusa. Policzmy go jednak z rozwinięcia Laplace’a. Najpierw utwórzmy w tym wyznaczniku więcej zer. Pamiętajmy, nie są to konieczne przekształcenia.

$\dpi{120} =\begin{vmatrix} 1 & -2 & 2\\ -1& 4& -2\\ -2& 2 &7 \end{vmatrix}\overset{IIk+IIIk}{=}\begin{vmatrix} 1 & -2 & 2+\left ( -2 \right )\\ -1 & 4 &-2+4 \\ -2 & 2& 7+2 \end{vmatrix}=$

$\dpi{120} =\begin{vmatrix} 1 & -2& 0\\ -1 & 4 & 2\\ -2 & 2 & 9 \end{vmatrix}\overset{Ik\cdot 2+IIk}{=}\begin{vmatrix} 1 & -2+2\cdot 1& 0\\ -1 & 4+2\cdot \left ( -1 \right ) & 2\\ -2& 2+2\cdot \left ( -2 \right ) & 9 \end{vmatrix}=$

$\dpi{120} =\begin{vmatrix} 1 & 0& 0\\ -1 & 2 & 2\\ -2& -2& 9 \end{vmatrix}$

Stosujemy rozwinięcie Laplace’a względem pierwszego wiersza:

$\dpi{120} \begin{vmatrix} {\color{Red} 1} & 0 & 0\\ -1& {\color{Blue} 2}&{\color{Blue} 2 }\\ -2& {\color{Blue} -2} & {\color{Blue} 9} \end{vmatrix}=\overset{1}{\overbrace{{\color{Red} 1}\cdot \left ( -1 \right )^{1+1}}}\begin{vmatrix} {\color{Blue} 2} &{\color{Blue} 2}\\ {\color{Blue} -2}& {\color{Blue} 9} \end{vmatrix}=2\cdot 9-2\cdot \left ( -2 \right )=18+4=22$ .

Pokaż rozwiązanie

Zwiń

h) $\dpi{120} \begin{vmatrix} 1 & 3 & 2 & 1 &4 \\ 2 & 1 & 5 & 1 & 2\\ 3 & 4 & 1 & 0 & 1\\ 2 &1 & 1 & 5 & 2\\ 3 & -1 &1 & -1 &1 \end{vmatrix}$ ,

Rozwiązanie

Wybierzmy np. czwartą kolumnę, w której utworzymy dodatkowe zera.

$\dpi{120} \begin{vmatrix} 1 & 3 & 2 & 1 &4 \\ 2 & 1 & 5 & 1 & 2\\ 3 & 4 & 1 & 0 & 1\\ 2 &1 & 1 & 5 & 2\\ 3 & -1 &1 & -1 &1 \end{vmatrix}\overset{Iw\cdot \left ( -1 \right )+IIw}{=}$

$\dpi{120} \overset{Iw\cdot \left ( -1 \right )+IIw}{=}\begin{vmatrix} 1 & 3 & 2 & 1& 4\\ 2+\left ( -1 \right )\cdot 1& 1+\left ( -1 \right )\cdot 3 & 5+\left ( -1 \right ) \cdot 2& 1+\left ( -1 \right )\cdot 1 & 2+\left ( -1 \right )\cdot 4\\ 3& 4& 1& 0& 1\\ 2& 1& 1& 5& 2\\ 3& -1& 1& -1 & 1 \end{vmatrix}=$

$\dpi{120} =\begin{vmatrix} 1 & 3& 2& 1& 4\\ 1& -2& 3 & 0 & -2\\ 3& 4& 1& 0 & 1\\ 2& 1& 1& 5& 2\\ 3& -1& 1 & -1& 1 \end{vmatrix}\overset{Ik\cdot \left ( 5 \right )+IVk}{=}$

$\dpi{120} \overset{Ik\cdot \left ( 5 \right )+IVk}{=}\begin{vmatrix} 1 & 3 & 2 & 1 & 4\\ 1& -2& 3 & 0 & -2\\ 3& 4& 1& 0&1 \\ 2+\left ( -5 \right )\cdot 1& 1+\left ( -5 \right )\cdot 3 & 1+\left ( -5 \right ) \cdot 2& 5+\left ( -5 \right )\cdot 1&2+\left ( -5 \right ) \cdot 4\\ 3 & -1& 1& -1& 1 \end{vmatrix}=$

$\dpi{120} =\begin{vmatrix} 1& 3 & 2& 1 & 4\\ 1& -2& 3& 0& -2\\ 3& 4 & 1& 0& 1\\ -3& -14 & -9& 0 & -18\\ 3& -1& 1& -1& 1 \end{vmatrix}\overset{Ik+Vk}{=}$

$\dpi{120} \overset{Ik+Vk}{=}\begin{vmatrix} 1& 3 & 2 & 1 & 4\\ 1& -2 & 3 & 0& -2\\ 3& 4 & 1 & 0 & 1\\ -3& -14& -9 & 0& -18\\ 3+1& -1+3& 1+2 & -1+1&1+4 \end{vmatrix}=$

$\dpi{120} =\begin{vmatrix} 1 & 3& 2 & 1& 4\\ 1& -2& 3 & 0& -2\\ 3& 4& 1 & 0& 1\\ -3& -14 & -9 & 0 & -18\\ 4& 2& 3 & 0 & 5 \end{vmatrix}=$

Stosujemy rozwinięcie Laplace’a względem pierwszego wiersza:

$\dpi{120} =\begin{vmatrix} 1 & 3& 2 & {\color{Red} 1}& 4\\ {\color{Blue} 1}& {\color{Blue} -2}& {\color{Blue} 3} & 0& {\color{Blue} -2}\\ {\color{Blue} 3}& {\color{Blue} 4}& {\color{Blue} 1} & 0&{\color{Blue} 1}\\ {\color{Blue} -3}& {\color{Blue} -14} & {\color{Blue} -9} & 0 & {\color{Blue} -18}\\ {\color{Blue} 4}& {\color{Blue} 2}& {\color{Blue} 3} & 0 & {\color{Blue} 5} \end{vmatrix}=\: \overset{-1}{\overbrace{{\color{Red} 1}\cdot \left ( -1 \right )^{1+4}}}\begin{vmatrix} {\color{Blue} 1} & {\color{Blue} -2} & {\color{Blue} 3 }& {\color{Blue} -2}\\ {\color{Blue} 3} & {\color{Blue} 4}& {\color{Blue} 1} & {\color{Blue} 1}\\ {\color{Blue} -3}& {\color{Blue} -14} & {\color{Blue} -9} & {\color{Blue} -18}\\ {\color{Blue} 4}& {\color{Blue} 2}& {\color{Blue} 3} &{\color{Blue} 5} \end{vmatrix}=$

$\dpi{120} =-1\cdot \begin{vmatrix} 1 & -2& 3& -2\\ 3& 4& 1 & 1\\ -3 & -14 & -9 & -18\\ 4& 2& 3 & 5 \end{vmatrix}=$

Wybierzmy pierwszą kolumnę, w której utworzymy kolejne zera:

$\dpi{120} =-1\cdot \begin{vmatrix} 1& -2& 3 & -2\\ 3 & 4 & 1 & 1\\ -3& -14 & -9 & -18\\ 4 & 2& 3 & 5 \end{vmatrix}\overset{Iw\cdot \left ( -3 \right )+IIw}{=}$

$\dpi{120} \overset{Iw\cdot \left ( -3 \right )+IIw}{=}\begin{vmatrix} 1 & -2 & 3 & -2\\ 3+\left ( -3 \right )\cdot 1& 4+\left ( -3 \right )\cdot \left ( -2 \right ) & 1+\left ( -3 \right )\cdot 3 & 1+\left ( -3 \right )\cdot \left ( -2 \right )\\ -3& -14 & -9 & -18\\ 4& 2& 3 & 5 \end{vmatrix}=$

$\dpi{120} =-1\cdot \begin{vmatrix} 1 & -2 & 3 & -2\\ 0& 10 & -8 & 7\\ 0& -20& 0 & -24\\ 4& 2 & 3 & 5 \end{vmatrix}\overset{Iw\cdot \left ( -4 \right )+IVw}{=}$

$\dpi{120} \overset{Iw\cdot \left ( -4 \right )+IVw}{=}-1\cdot \begin{vmatrix} 1& -2 & 3& -2\\ 0& 10& -8 & 7\\ 0& -20& 0& -24\\ 4+\left ( -4 \right )\cdot 1& 2+\left ( -4 \right )\cdot \left ( -2 \right ) &3+\left ( -4 \right ) \cdot 3 & 5+\left ( -4 \right )\cdot \left ( -2 \right ) \end{vmatrix}=$

$\dpi{120} =-1\cdot \begin{vmatrix} 1 & -2& 3& -2\\ 0 & 10 & -8 & 7\\ 0& -20 & 0 & -24\\ 0& 10& -9 & 13 \end{vmatrix}=$

Stosujemy rozwinięcie Laplace’a względem pierwszego wiersza:

$\dpi{120} ={\color{Red} -1}\cdot \begin{vmatrix} {\color{Green} 1} & -2& 3& -2\\ 0 & {\color{Blue} 10} & {\color{Blue} -8} &{\color{Blue} 7}\\ 0& {\color{Blue} -20 }& {\color{Blue} 0} & {\color{Blue} -24}\\ 0& {\color{Blue} 10}& {\color{Blue} -9} & {\color{Blue} 13} \end{vmatrix}=\overset{-1}{\overbrace{{{\color{Red} -1}\cdot {\color{Green} 1}\cdot \left ( -1 \right )^{1+1}}}}\cdot \begin{vmatrix} {\color{Blue} 10} & {\color{Blue} -8}& {\color{Blue} 7}\\ {\color{Blue} -20}& {\color{Blue} 0}& {\color{Blue} -24}\\ {\color{Blue} 10}& {\color{Blue} -9}& {\color{Blue} 13} \end{vmatrix}=$

$\dpi{120} =-1\cdot \begin{vmatrix} 10 & -8 & 7\\ -20& 0 &-24 \\ 10 & -9 & 13 \end{vmatrix}\begin{matrix} 10 & -8\\ -20 & 0\\ 10& -9 \end{matrix}=$

$\dpi{120} =-1\cdot \left [ 10\cdot 0\cdot 13+\left ( -8 \right )\cdot \left ( -24 \right ) \cdot 10+7\cdot \left ( -20 \right )\cdot \left ( -9 \right )-\left ( -8 \right )\cdot \left ( -20 \right )\cdot 13-10\cdot \left ( -24 \right )\cdot \left ( -9 \right )-7\cdot 0\cdot 10\right ]=$

$\dpi{120} =-1\cdot \left ( 0+1920+1260-2080-2160-0 \right )=-1\cdot \left ( -1060 \right )=1060$

Pokaż rozwiązanie

Zwiń

i) $\dpi{120} \begin{vmatrix} 1 & -1 & 2 & 0 &3 \\ 2& -2 & -5 &1 & 1\\ 4& -3 & 4 & 1 & 2\\ 1& 1 & 2 & -1 &2 \\ 2 &-1 & 0 & 1&3 \end{vmatrix}$ .

Rozwiązanie

Wybierzmy czwartą kolumnę i utwórzmy w niej dodatkowe zera. Działania przeprowadzamy wówczas na wierszach.

$\dpi{120} \begin{vmatrix} 1 & -1 & 2 & 0 &3 \\ 2& -2 & -5 &1 & 1\\ 4& -3 & 4 & 1 & 2\\ 1& 1 & 2 & -1 &2 \\ 2 &-1 & 0 & 1&3 \end{vmatrix}\overset{IVw+IIw}{=}\begin{vmatrix} 1 & -1& 2& 0& 3\\ 2+1& -2+1& -5+2& 1+\left ( -1 \right ) & 1+2\\ 4& -3& 4& 1 & 2\\ 1& 1& 2& -1& 2\\ 2& -1& 0 & 1 & 3 \end{vmatrix}=$

$\dpi{120} =\begin{vmatrix} 1 & -1& 2 & 0& 3\\ 3& -1& -3& 0&3 \\ 4& -3& 4 & 1& 2\\ 1& 1& 2 & -1& 2\\ 2& -1& 0& 1 & 3 \end{vmatrix}\overset{IVw+IIIw}{=}\begin{vmatrix} 1 & -1& 2& 0& 3\\ 3& -1& -3& 0 &3 \\ 4+1& -3+1& 4+2& 1+\left ( -1 \right )&2+2 \\ 1 & 1& 2 & -1 & 2\\ 2& -1 & 0& 1&3 \end{vmatrix}=$

$\dpi{120} =\begin{vmatrix} 1& -1& 2 & 0 & 3\\ 3& -1 & -3& 0& 3\\ 5& -2& 6& 0& 4\\ 1 & 1& 2& -1& 2\\ 2& -1& 0& 1 & 3 \end{vmatrix}\overset{IVw+Vw}{=}\begin{vmatrix} 1 & -1& 2& 0& 3\\ 3& -1 & -3 & 0& 3\\ 5& -2 & 6 & 0& 4\\ 1& 1& 2 & -1 & 2\\ 2+1& -1+1& 0+2& 1+\left ( -1 \right ) &3+2 \end{vmatrix}=$

$\dpi{120} =\begin{vmatrix} 1 & -1& 2 & 0 &3 \\ 3 & -1 & -3 & 0&3 \\ 5& -2& 6& 0& 4\\ 1 & 1& 2& -1& 2\\ 3& 0& 2& 0 & 5 \end{vmatrix}=$

Stosujemy rozwinięcie Laplace’a względem czwartej kolumny:

$\dpi{120} =\begin{vmatrix} {\color{Blue} 1 }& {\color{Blue} -1}& {\color{Blue} 2} & 0 &{\color{Blue} 3} \\ {\color{Blue} 3} & {\color{Blue} -1} & {\color{Blue} -3} & 0&{\color{Blue} 3} \\ {\color{Blue} 5}& {\color{Blue} -2}&{\color{Blue} 6}& 0& {\color{Blue} 4}\\ 1 & 1& 2& {\color{Red} -1}& 2\\ {\color{Blue} 3}& {\color{Blue} 0}& {\color{Blue} 2}& 0 &{\color{Blue} 5} \end{vmatrix}=\overset{-1}{{\overbrace{{\color{Red} -1}\cdot \left ( -1 \right )^{4+4}}}}\cdot \begin{vmatrix}{\color{Blue} 1 }& {\color{Blue} -1}& {\color{Blue} 2}& {\color{Blue} 3}\\ {\color{Blue} 3} & {\color{Blue} -1}& {\color{Blue} -3}& {\color{Blue} 3}\\ {\color{Blue} 5}& {\color{Blue} -2}& {\color{Blue} 6}& {\color{Blue} 4}\\ {\color{Blue} 3}& {\color{Blue} 0}& {\color{Blue} 2} &{\color{Blue} 5} \end{vmatrix}=$

$\dpi{120} =-1\cdot \begin{vmatrix} 1 & -1& 2 & 3\\ 3 & -1& -3& 3\\ 5 & -2 & 6 & 4\\ 3& 0&2 &5 \end{vmatrix}=$

Utwórzmy zera w drugiej kolumnie:

$\dpi{120} \overset{Iw\cdot \left ( -1 \right )+IIw}{=}\begin{vmatrix} 1 & -1& 2 & 3\\ 3+\left ( -1 \right )\cdot 1& -1+\left ( -1 \right )\cdot \left ( -1 \right )& -3+\left ( -1 \right )\cdot 2 &3+\left ( -1 \right )\cdot 3 \\ 5& -2 & 6 & 4\\ 3& 0 & 2 &5 \end{vmatrix}=$

$\dpi{120} =-1\cdot \begin{vmatrix} 1 & -1& 2 & 3\\ 2& 0& -5& 0\\ 5& -2& 6& 4\\ 3& 0& 2& 5 \end{vmatrix}=$

$\dpi{120} \overset{Iw\cdot \left ( -2 \right )+IIIw}{=}-1\cdot \begin{vmatrix} 1 & -1& 2 & 3\\ 2& 0& -5& 0\\ 5+\left ( -2 \right )\cdot 1& -2+\left ( -2 \right )\cdot \left ( -1 \right )& 6+\left ( -2 \right )\cdot 2 & 4+\left ( -2 \right )\cdot 3\\ 3& 0& 2 &5 \end{vmatrix}=$

$\dpi{120} =-1\cdot \begin{vmatrix} 1& -1& 2& 3\\ 2& 0 & -5& 0\\ 3& 0& 2& -2\\ 3& 0 & 2 &5 \end{vmatrix}=$

Stosujemy rozwinięcie Laplace’a względem drugiej kolumny:

$\dpi{120} ={\color{Red} -1}\cdot \begin{vmatrix} 1& {\color{Green} -1}& 2& 3\\ {\color{Blue} 2}& 0 & {\color{Blue} -5}& {\color{Blue} 0}\\ {\color{Blue} 3}& 0& {\color{Blue} 2}& {\color{Blue} -2}\\ {\color{Blue} 3}& 0 & {\color{Blue} 2} &{\color{Blue} 5} \end{vmatrix}=\overset{-1}{\overbrace{{\color{Red} -1}\cdot \left ( {\color{Green} -1} \right )\cdot \left ( -1 \right )^{1+2}}}\cdot \begin{vmatrix} {\color{Blue} 2} &{\color{Blue} -5} &{\color{Blue} 0} \\ {\color{Blue} 3}& {\color{Blue} 2} &{\color{Blue} -2} \\ {\color{Blue} 3}& {\color{Blue} 2} & {\color{Blue} 5} \end{vmatrix}=$

$\dpi{120} =-1\cdot \begin{vmatrix} 2 & -5& 0\\ 3& 2& -2\\ 3& 2 & 5 \end{vmatrix}\begin{matrix} 2 & -5\\ 3& 2\\ 3& 2 \end{matrix}=$

$\dpi{120} =-1\cdot \left [ 2\cdot 2\cdot 5+\left ( -5 \right ) \cdot \left ( -2 \right )\cdot 3+0\cdot 3\cdot 2-\left ( -5 \right )\cdot 3\cdot 5-2\cdot \left ( -2 \right )\cdot 2-0\cdot 2\cdot 3\right ]=$

$\dpi{120} =-1\cdot \left ( 20+30+0+75+8-0 \right )=-1\cdot 133=-133$

Pokaż rozwiązanie

Zwiń

Zadania 4.-7. są niestandardowe, ale warto je przestudiować. Rozwiązania są krótkie.

Zadanie 4. Niech macierze $\dpi{120} \large A,B,C$ będą macierzami kwadratowymi trzeciego stopnia takimi, że $\dpi{120} \large \det A=1,\det B=3,\det C=2.$ Obliczyć $\dpi{120} \large \det (4BC^{T}\, A).$

Rozwiązanie

1. Z własności: $\dpi{120} \det \left ( \alpha \cdot A \right )=\alpha ^{n}\cdot A\: ,\: \alpha \in R$ , $\dpi{120} n -$ stopień macierzy $\dpi{120} A$ ( nas $\dpi{120} n={\color{Blue} 3}$ ) mamy, że

$\dpi{120} \det \left ( {\color{Red} 4}BC^{T}A \right )={\color{Red} 4}^{{\color{Blue} 3}} \det \left ( BC^{T} A\right )$

2. Z własności: $\dpi{120} \det \left ( A\cdot B \right )= \det A\cdot \det B$ otrzymujemy:

$\dpi{120} 4^{3}\det \left ( BC^{T}A \right )=4^{3} \det B\cdot \det C^{T}\cdot \det A$

3. Z własności: $\dpi{120} \det A= \det A^{T}$ mamy, że $\dpi{120} \det C^{T}= \det C$ , a więc

$\dpi{120} 4^{3}\det B\cdot \det C^{T}\cdot \det A=4^{3} \det B\cdot \det C\cdot \det A=4^{3}\cdot 3\cdot 2\cdot 1=384$

Pokaż rozwiązanie

Zwiń

Zadanie 5. Niech $\dpi{120} \large A,B,C\in M_{4}(\mathbb{R})$ oraz $\dpi{120} \large \det A=-3,\det B=2,\det C=-1.$ Obliczyć $\dpi{120} \large \det (C^{T}\cdot A^{2}\cdot 3B).$

Rozwiązanie

1. Z własności: $\dpi{120} \det \left ( A\cdot B \right )= \det A\cdot \det B$ otrzymujemy:

$\dpi{120} \det \left ( C^{T} A^{2}3B\right )= \det C^{T}\cdot \det A^{2} \cdot \det 3B= \det C^{T}\cdot \det \left ( A\cdot A \right )\cdot \det 3B=$

$\dpi{120} =\det C^{T}\cdot \det A\cdot \det A\cdot \det 4B= \det C^{T}\cdot \left ( \det A\right )^{2}\cdot \det 4B$

2. Z własności: $\dpi{120} \det \left ( \alpha \cdot A \right )=\alpha ^{n}\cdot \det A\, ,\alpha \in R$ , $\dpi{120} n$ – stopień macierzy $\dpi{120} A$ mamy, że (u nas $\dpi{120} n={\color{Green} 4}$ ):

$\dpi{120} \det C^{T}\cdot \left ( \det A \right )^{2}\cdot \det {\color{Red} 3}B= \det C^{T}\cdot \left ( \det A \right )^{2}\cdot {\color{Red} 3}^{{\color{Green} 4}} \det B=$

$\dpi{120} =\left ( -1 \right )\cdot \left ( -3 \right )^{2}\cdot 3^{4}\cdot 2=-1458$

Pokaż rozwiązanie

Zwiń

Zadanie 6. Nie obliczając wartości wyznacznika, znaleźć liczbę $\dpi{120} \large x$ spełniającą równanie

$\dpi{120} \begin{vmatrix} 1+x & 1 &1 & 1\\ 2 & 2 &2 & 2\\ 4 & 6-x & 4 & 4\\ 6 & 6 & 6 &x \end{vmatrix}=0.$

Rozwiązanie:

Wyznacznik jest równy zero, gdy dwa wiersze (kolumny) są sobie równe. Zauważmy, że aby wyznacznik był równy zero, wystarczy, aby dwie z kolumn były postaci $\dpi{120} \begin{vmatrix} 1\\ 2 \\ 4 \\ 6 \end{vmatrix}$ . Otrzymujemy, że:

$\dpi{120} 1+x=1\; \; \vee \; \; 6-x=4\; \; \vee \; \; x=6$

Stąd:

$\dpi{120} x_{1}=0\; \; \vee \; \; x_{2}=2\; \; \vee \; \; x_{3}=6$

Wartości te są rozwiązaniami równania.

Pokaż rozwiązanie

Zwiń

Zadanie 7. Nie obliczając wyznaczników $\dpi{120} \begin{vmatrix} 2 &4 &7 \\ 8 & 6 &3 \\ 2& 1 &5 \end{vmatrix},\begin{vmatrix} 8 &3 &9 \\ 2 & 4 &8 \\ 3&1 &7 \end{vmatrix}$ wykazać, że dzielą się przez 10.

Rozwiązanie:

Zapiszmy wyznacznik macierzy $\dpi{120} \begin{vmatrix} 2 & 4 & 7\\ 8& 6 & 3\\ 2 & 1 & 5 \end{vmatrix}$ w innej postaci.

$\dpi{120} \begin{vmatrix} 2 & 4 & 7\\ 8& 6 & 3\\ 2 & 1 & 5 \end{vmatrix}=\begin{vmatrix} 2 & 4 & 7\\ 10-2& 10-4 &10-7 \\ 2& 1& 5 \end{vmatrix}=$

Korzystamy z własności wyznacznika:

$\dpi{120} \det \left ( A_{1},...,A_{i} +\alpha A_{j},...,A_{j},...,A_{n}\right )=\det \left ( A_{1} ,...,A_{i},...,A_{j},...,A_{n}\right )$ dla $\dpi{120} i\neq j\: ,\: \alpha \in \mathbb{R}$ .

Mamy, że

$\dpi{120} =\begin{vmatrix} 2 & 4& 7\\ 10-2& 10-4& 10-7\\ 2& 1& 5 \end{vmatrix}=\begin{vmatrix} 2 & 4& 7\\ 10& 10&10 \\ 2&1 & 5 \end{vmatrix}=$

$\dpi{120} =10\cdot \begin{vmatrix} 2 & 4 & 7\\ 1& 1& 1\\ 2& 1& 5 \end{vmatrix}$ .

Wyznacznik $\dpi{120} \begin{vmatrix} 2 & 4& 7\\ 1& 1 &1 \\ 2& 1& 5 \end{vmatrix}$ jest liczbą całkowitą, więc $\dpi{120} \begin{vmatrix} 2 & 4& 7\\ 8& 6 & 3\\ 2& 1 & 5 \end{vmatrix}$ jest podzielny przez 10.

Analogicznie rozpisujemy wyznacznik $\dpi{120} \begin{vmatrix} 8 & 3& 9\\ 2 & 4 & 8\\ 3& 1& 7 \end{vmatrix}$ .

$\dpi{120} \begin{vmatrix} 8 & 3& 9\\ 2 & 4 & 8\\ 3& 1& 7 \end{vmatrix}=\begin{vmatrix} 8 & 3& 9\\ 2+3& 4+1 & 8+7\\ 3& 1 & 7 \end{vmatrix}=\begin{vmatrix} 8 & 3&9 \\ 5& 5 & 15\\ 3& 1 & 7 \end{vmatrix}=$

$\dpi{120} =5\cdot \begin{vmatrix} 8& 3 & 9\\ 1& 1 & 3\\ 3& 1 & 7 \end{vmatrix}=5\cdot \begin{vmatrix} 8 & 3& 9-3\\ 1& 1&3-1 \\ 3& 1& 7-1 \end{vmatrix}=5\cdot \begin{vmatrix} 8 & 3 & 6\\ 1& 1& 2\\ 3& 1 & 6 \end{vmatrix}=$

$\dpi{120} =5\cdot 2\cdot \begin{vmatrix} 8 & 3 &3 \\ 1 & 1 & 1\\ 3 & 1 & 3 \end{vmatrix}=10\cdot \begin{vmatrix} 8 & 3 & 3\\ 1& 1 &1 \\ 3& 1 & 3 \end{vmatrix}$ .

Wyznacznik $\dpi{120} \begin{vmatrix} 8 & 3& 3\\ 1& 1 & 1\\ 3& 1 & 3 \end{vmatrix}$ jest liczbą całkowitą, więc $\dpi{120} \begin{vmatrix} 8& 3& 9\\ 2 & 4& 8\\ 3 & 1 & 7 \end{vmatrix}$ jest podzielny przez 10.

Pokaż rozwiązanie

Zwiń