Warto zapoznać się z zakładką Wzory tutaj i Teoria tutaj.
Zadanie 1. Zbadać monotoniczność funkcji:
1)
Rozwiązanie
Pamiętajmy, że pomimo tego, że w zadaniu nie ma nic napisane o dziedzinie funkcji, wyznaczenie jej jest rzeczą konieczną.
W naszym przypadku: .
Teraz możemy przystąpić do liczenia pochodnej. Zatem:
Najpierw jednak przekształćmy funkcję:
Wracamy do pochodnej:
Rozwiązujemy nierówność np.
,
,
.
Stąd wynika, że
1) dla funkcja
, a stąd wynika, że
jest rosnąca.
2) dla funkcja
, a stąd wynika, że
jest malejąca.
Gdzie domkniemy nawiasy, nie ma znaczenia.
2)
Rozwiązanie
1. Wyznaczamy dziedzinę.
Wyrażenie podpierwiastkowe musi być nieujemne, więc:
Zatem: .
2. Liczymy pochodną:
sprowadzamy do wspólnego mianownika
3. Badamy znak pochodnej. Zależy on tylko od licznika, ponieważ mianownik jest stale dodatni. Zatem:
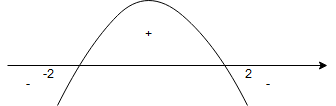
Dostaliśmy, że:
dla
,
dla
.
Musimy jeszcze uwzględnić dziedzinę funkcji . Stąd:
- dla
pochodna
, a zatem funkcja jest malejąca
- dla
pochodna
, a zatem funkcja jest rosnąca.
3)
Rozwiązanie
1. Dziedzina: .
2. Pochodna:
3. Badamy znak pochodnej:
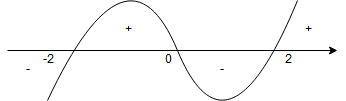
– dla
,
– dla
.
4. Monotoniczność:
– dla funkcja
jest rosnąca,
– dla funkcja
jest malejąca.
4)
Rozwiązanie
1. Dziedzina: .
2. Pochodna:
3. Badamy znak pochodnej.
Znak pochodnej zależy jedynie od czynnika
, gdyż
dla dowolnego
.
Czyli:
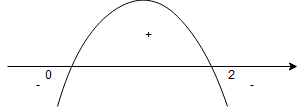
– dla
,
– dla
.
4. Monotoniczność:
– dla funkcja
jest rosnąca,
– dla funkcja
jest malejąca.
5)
Rozwiązanie
1. Dziedzina: .
2. Pochodna:
3. Badamy znak pochodnej.
Znak pochodnej zależy jedynie od czynnika
, gdyż
dla dowolnego
.
Czyli:
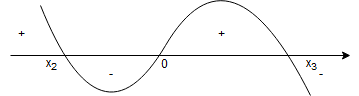
– dla
,
– dla
.
4. Monotoniczność:
– dla funkcja
jest rosnąca,
– dla funkcja
jest malejąca.
6)
Rozwiązanie
1. Dziedzina: . Pamiętajmy dziedziną logarytmu jest
, ponadto mianownik musi być różny od zera, czyli
.
2. Pochodna:
3. Badamy znak pochodnej.
Znak pochodnej zależy jedynie od licznika
, gdyż
dla dowolnego
.
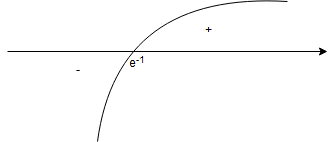
– dla
,
– dla
.
Uwzględniliśmy tutaj dziedzinę funkcji.
4. Monotoniczność:
– dla funkcja
jest rosnąca,
– dla funkcja
jest malejąca.
Zadanie 2. Znaleźć przedziały, na których wykres funkcji jest wypukły bądź wklęsły oraz wyznaczyć punkty przegięcia tego wykresu.
1)
Rozwiązanie
1. Dziedzina funkcji . Liczymy pierwszą pochodną:
2. Liczymy drugą pochodną:
3. Badamy znak drugiej pochodnej:
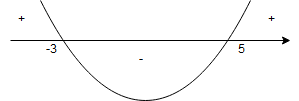
– dla
– dla
.
Wynika stąd, że :
– funkcja jest wypukła dla
– funkcja jest wklęsła dla
.
W punktach
oraz
druga pochodna zmienia znak, czyli są to punkty przegięcia.
2)
Rozwiązanie
1. Dziedzina funkcji . Liczymy pierwszą pochodną:
2. Liczymy drugą pochodną:
3. Badamy znak drugiej pochodnej:
Ponieważ , to
dla dowolnego
.
Wynika stąd, że funkcja jest wypukła w całej dziedzinie: . Nie posiada punktów przegięcia.
3)
Rozwiązanie
1. Dziedzina funkcji . Liczymy pierwszą pochodną:
2. Liczymy drugą pochodną:
3. Badamy znak drugiej pochodnej:
Stąd:
– dla
– dla
.
Wynika stąd, że :
– funkcja jest wypukła dla
– funkcja jest wklęsła dla
.
Druga pochodna nie zeruje się w żadnym punkcie, więc funkcja nie ma punktów przegięcia.
4)
Rozwiązanie
1. Dziedzina funkcji . Liczymy pierwszą pochodną:
Policzyliśmy tutaj pochodną z funkcji złożonej, można ją również liczyć ze wzoru na pochodną z ilorazu. Pamiętajmy .
2. Liczymy drugą pochodną:
3. Badamy znak drugiej pochodnej.
Ponieważ mianownik jest dodatni, więc znak drugiej pochodnej zależy jedynie od licznika.
Stąd:
– dla
,
– dla
.
Wynika stąd, że :
– funkcja jest wypukła dla
,
– funkcja jest wklęsła dla
.
W punktach
oraz
druga pochodna zmienia znak, czyli są to punkty przegięcia.
Zadanie 3. Znaleźć asymptoty funkcji:
1)
Rozwiązanie
1. Dziedzina funkcji: . Wnioskujemy stąd, że są dwie asymptoty pionowe:
oraz
2. Badamy istnienie asymptot poziomych. W tym celu liczymy:
oraz
Ponieważ obydwie granice są skończone i równają się , więc mamy asymptotę poziomą:
3. Ponieważ otrzymaliśmy asymptotę poziomą, wnioskujemy, że asymptot ukośnych brak.
2)
Rozwiązanie
1. Dziedzina funkcji: . Stąd mamy jedną asymptotę pionową:
2. Sprawdzamy istnienie asymptot poziomych:
zaś
co pokazuje, że asymptot poziomych nie ma.
3. Szukamy zatem asymptoty ukośnej .
Pamiętamy, że przy tego typu granicach wystarczy spojrzeć na współczynniki przy najwyższych potęgach licznika i mianownika.
Zatem asymptota ukośna ma równanie: .
3)
Rozwiązanie
1. Dziedzina funkcji: .Wnioskujemy stąd, że są dwie asymptoty pionowe:
oraz
2. Badamy istnienie asymptot poziomych. W tym celu liczymy:
oraz
Zatem asymptot poziomych brak.
3. Szukamy zatem asymptoty ukośnej .
Równanie asymptoty ukośnej: .
4)
Rozwiązanie
1. Dziedzina funkcji: .Wnioskujemy stąd, że są dwie asymptoty pionowe:
oraz
2. Badamy istnienie asymptot poziomych. W tym celu liczymy:
Zatem istnieje asymptota pozioma .
3. Asymptot ukośnych nie ma, gdyż istniała asymptota pozioma.