Liczbą zespoloną nazywamy uporządkowaną parę liczb rzeczywistych . Parę taką zapisujemy jako:
Postać tę nazywamy postacią algebraiczną (kanoniczną) liczby zespolonej. Liczba to tzw. część rzeczywista, zaś
część urojona liczby zespolonej
i oznaczamy:
Symbol oznacza jednostkę urojoną spełniającą warunek:
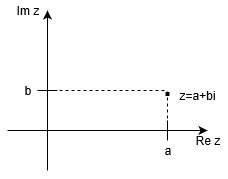
Na zbiorze – wszystkich liczb zespolonych określamy podstawowe działania: dodawanie, odejmowanie, mnożenie i dzielenie.
Niech oraz
– Dodawanie:
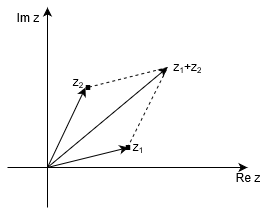
– Odejmowanie:
– Mnożenie:
(mnożymy jak wielomiany)
(pamiętamy:
)
– Dzielenie:
Wprowadźmy tzw. liczbę sprzężoną z liczbą
. Dla
liczba z nią sprzężona to
Wróćmy do dzielenia liczb zespolonych.
(mnożymy licznik i mianownik przez sprzężenie mianownika)
(grupujemy część rzeczywistą i urojoną)
przy założeniu, że , czyli
, a stąd
oraz
.
Dwie liczby zespolone i
są równe, gdy równe są ich części rzeczywiste oraz urojone, tzn.
Zapraszamy do zadań! tutaj