Całka jako pole obszaru (teoria) - WYZNACZNIK

Dana jest funkcja $\dpi{120} f:X\rightarrow \mathbb{R}$ ciągła w przedziale $\dpi{120} \left \langle a;b \right \rangle\subset X$ .

Całką oznaczoną funkcji $\dpi{120} f$ w przedziale $\dpi{120} \left \langle a;b \right \rangle$ nazywamy różnicę wartości dowolnej funkcji pierwotnej $\dpi{120} F\left ( x \right )$ na końcach przedziału całkowania, co zapisujemy następująco:

$całka oznaczona$

Liczbę $\dpi{120} a$ nazywamy dolną granicą całkowania, zaś $\dpi{120} b$ – górną granicą całkowania.

Jeżeli istnieje $\dpi{120} \int_{a}^{b}f\left ( x \right )dx$ , to mówimy, że funkcja $\dpi{120} f$ jest całkowalna w przedziale $\dpi{120} \left \langle a;b \right \rangle$ .

Podstawowe własności całek oznaczonych:

1. $\dpi{120} \int_{a}^{b}\left ( f\left ( x \right ) \pm g\left ( x \right )\right )dx=\int_{a}^{b}f\left ( x \right )dx\pm \int_{a}^{b}g\left ( x \right )dx$

2. $\dpi{120} \int_{a}^{b}cf\left ( x \right )dx=c\int_{a}^{b}f\left ( x \right )dx,\; \; \; c\in \mathbb{R}$

3. $\dpi{120} \int_{a}^{a}f\left ( x \right )dx=0$

4. $\dpi{120} \int_{a}^{b}f\left ( x \right )dx=-\int_{b}^{a}f\left ( x \right )dx$

5. $\int_{a}^{b}f\left ( x \right )dx+ \int_{b}^{c}f\left ( x \right )dx=\int_{a}^{c}f\left ( x \right )dx$

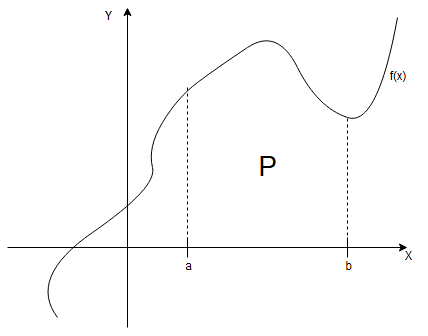
Jeżeli w przedziale $\dpi{120} \left \langle a;b \right \rangle$ funkcja $\dpi{120} f\left ( x \right )\geqslant 0$ , to $\dpi{120} \int_{a}^{b}f\left ( x \right )dx$ oznacza pole obszaru ograniczonego łukiem krzywej $\dpi{120} y=f\left ( x \right )$ , osią $\dpi{120} Ox$ oraz prostymi $\dpi{120} x=a$ i $\dpi{120} x=b$ . Jeżeli zaś $\dpi{120} f\left ( x \right )\leqslant 0$ w przedziale $\dpi{120} \left \langle a;b \right \rangle$ to pole opisanego wyżej obszaru jest równe $\dpi{120} -\int_{a}^{b}f\left ( x \right )dx$ .

pole obszaru jako całka

Zawsze więc pole obszaru, o którym mowa wyraża się całką oznaczoną:

$całka jako pole obszaru$

Zapraszamy do zadań! tutaj