1. Sprowadzamy liczbę do postaci trygonometrycznej (patrz algorytm sprowadzania liczby zespolonej do postaci trygonometrycznej w zakładce wzory w temacie Postać trygonometryczna tutaj).
2. Wykorzystujemy wzór:
![pierwiastkowanie liczb zespolonych \dpi{120} \sqrt[n]{z}=w_{k}=\sqrt[n]{\left | z \right |}\cdot \left ( \cos \frac{\varphi +2k\pi }{n}+i\sin \frac{\varphi +2k\pi }{n} \right ),\; k=0,1...,n-1,](http://latex.codecogs.com/gif.latex?\dpi{120}&space;\sqrt[n]{z}=w_{k}=\sqrt[n]{\left&space;|&space;z&space;\right&space;|}\cdot&space;\left&space;(&space;\cos&space;\frac{\varphi&space;+2k\pi&space;}{n}+i\sin&space;\frac{\varphi&space;+2k\pi&space;}{n}&space;\right&space;),\;&space;k=0,1...,n-1,)
wstawiając za 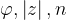 odpowiednie wartości z punktu 1.,
odpowiednie wartości z punktu 1., 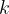 musi pozostać w zapisie.
musi pozostać w zapisie.
3. Wstawiamy kolejno wartości 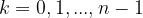 , skąd otrzymujemy
, skąd otrzymujemy 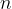 różnych pierwiastków. Dla każdego
różnych pierwiastków. Dla każdego 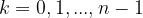 kolejność wykonywania czynności jest taka sama (kolejne kroki).
kolejność wykonywania czynności jest taka sama (kolejne kroki).
4. Dla konkretnego 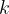 dodajemy wartości
dodajemy wartości 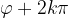 , a następnie dzielimy przez
, a następnie dzielimy przez 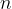 . Otrzymujemy ułamek, najpierw piętrowy (po dodawaniu), później go likwidujemy (dzielenie przez
. Otrzymujemy ułamek, najpierw piętrowy (po dodawaniu), później go likwidujemy (dzielenie przez 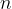 ).
).
5. Jeżeli dostaliśmy liczbę mniejszą bądź równą 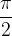 odczytujemy wartości sinusów i cosinusów z tabeli wartości trygonometrycznych (o ile to możliwe). Możemy bowiem otrzymać wartości kąta, których nie ma w podstawowej tabeli (będą w tablicach, ale nas to nie interesuje). Wówczas zostawiamy odpowiedź w postaci z sinusem i cosinusem. Koniec zadania.
odczytujemy wartości sinusów i cosinusów z tabeli wartości trygonometrycznych (o ile to możliwe). Możemy bowiem otrzymać wartości kąta, których nie ma w podstawowej tabeli (będą w tablicach, ale nas to nie interesuje). Wówczas zostawiamy odpowiedź w postaci z sinusem i cosinusem. Koniec zadania.
6. Jeżeli dostaliśmy liczbę większą od 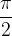 musimy zastosować wzory redukcyjne:
musimy zastosować wzory redukcyjne:
a) ustalamy ćwiartkę do której należy kąt
b) zapisujemy go tak, aby móc skorzystać ze wzorów redukcyjnych
c) stosujemy wzory redukcyjne
7. Odczytujemy wartości sinusów i cosinusów z tabeli wartości funkcji trygonometrycznych (o ile to możliwe). Koniec zadania.
. Pierwiastki
-tego stopnia liczby zespolonej
mają postać:
– moduł liczby zespolonej,
– kąt, tzw. argument główny liczby zespolonej, obliczamy z zależności:
liczby zespolonej