Mamy 4 zadania. Są one ułożone od łatwych do trudnych. Zadanie 1 ”przyzwyczaja” nas do dwóch zmiennych i do kolejności całkowania. Zadanie 2 to właściwie to samo co w zadaniu 1, ale inaczej sformułowane polecenie. Nie wymaga rysowania obszaru całkowania. W zadaniu 3 bardzo ważny jest poprawny wykres obszaru całkowania, z którego najczęściej możemy odczytać granice całkowania. Zadanie 4 to zastosowanie całek podwójnych do liczenia pól obszarów. Znowu istotną częścią zadania jest rysunek.
Zadanie 1. Obliczyć całki (tzw. iterowane):
1)
Rozwiązanie Zwróćmy uwagę na kolejność różniczek w całce. Mamy Liczymy całkę w nawiasie okrągłym: Pozostaje nam do policzenia całka pojedyncza po zmiennej , co wskazuje, że najpierw całkujmy po zmiennej
, a następnie po
. Przy pierwszym całkowaniu (po
) zmienną
traktujemy jak stałą. Znak pierwszej całki przepisujemy i wyłączamy
przed znak drugiej całki (jako stałą). Mamy:
:
2)
Rozwiązanie Zauważmy, że teraz kolejność różniczek Liczymy całkę w nawiasie okrągłym: Została nam całka pojedyncza po zmiennej Wykorzystaliśmy wzór (pojawił się przy całkowaniu przez części): jest inna niż w podpunkcie 1), co wskazuje, że najpierw liczymy całkę po zmiennej
, a później po zmiennej
. Zatem:
:
3)
Rozwiązanie Kolejność różniczek U nas ponieważ całkujemy po Ze wzoru redukcyjnego mamy wskazuje, że najpierw całkujemy po zmiennej
, a później po
. Zatem zmienną
traktujemy jak stałą. Wykorzystamy wcześniejszy wzór:
współczynnik:
i
. Zatem:
, więc
4)
Rozwiązanie Kolejność różniczek Liczymy całkę w nawiasie okrągłym: wskazuje, że najpierw liczymy całkę po zmiennej
, a później po zmiennej
. Zatem:
5)
Rozwiązanie Kolejność różniczek Ponieważ całkujemy po wskazuje, że najpierw całkujemy po zmiennej
, a później po
.Wykorzystujemy wzór:
, więc u nas
. Zatem:
6)
Rozwiązanie Kolejność różniczek U nas wskazuje, że najpierw całkujemy po zmiennej
, a później po
. Zatem zmienną
traktujemy jak stałą. Wykorzystujemy wzór:
. Mamy:
Zadanie 2. Obliczyć całkę podwójną w prostokącie:
1)
Rozwiązanie Ponieważ jest to całka po prostokącie nie ma potrzeby rysowania obszaru całkowania. Granice całkowania widzimy w zapisie prostokąta. Ponieważ obie granice są stałe, więc kolejność całkowania jest dowolna. Możemy zatem liczyć: Policzmy np. lub
. Druga z całek powinna wyjść dokładnie tyle samo. Zatem:
2)
Rozwiązanie Ponieważ jest to całka po prostokącie nie ma potrzeby rysowania obszaru całkowania. Granice całkowania widzimy w zapisie prostokąta. Ponieważ obie granice są stałe, więc kolejność całkowania jest dowolna. Możemy zatem liczyć: Policzmy np. Wykorzystamy wzór: U nas lub
. Mamy:
. Zatem:
3)
Rozwiązanie Ponieważ jest to całka po prostokącie nie ma potrzeby rysowania obszaru całkowania. Granice całkowania widzimy w zapisie prostokąta. Ponieważ obie granice są stałe, więc kolejność całkowania jest dowolna. Możemy zatem liczyć: Policzmy np. Zmienną lub
. Mamy:
traktujemy jak stałą, całkujemy najpierw względem zmiennej
:
4)
Rozwiązanie Ponieważ jest to całka po prostokącie nie ma potrzeby rysowania obszaru całkowania. Granice całkowania widzimy w zapisie prostokąta. Ponieważ obie granice są stałe, więc kolejność całkowania jest dowolna. Możemy zatem liczyć: W tym przykładzie łatwiej jest najpierw policzyć całkę po zmiennej Wykorzystujemy wzór: U nas Ze wzoru redukcyjnego mamy, że Całkę nieoznaczoną Wstawiamy do całki oznaczonej: lub
, gdyż po zmiennej
musielibyśmy użyć metody przez podstawienie. Ale oczywiście możemy zacząć również od takiego całkowania. My liczymy całkę:
, gdyż całkę liczymy po zmiennej
, a współczynnik przy
wynosi 1. Zatem:
. Zatem:
liczymy przez podstawienie.
5)
Rozwiązanie
Ponieważ jest to całka po prostokącie nie ma potrzeby rysowania obszaru całkowania. Granice całkowania widzimy w zapisie prostokąta. Ponieważ obie granice są stałe, więc kolejność całkowania jest dowolna. Możemy zatem liczyć:
lub
W tym przykładzie łatwiej jest najpierw policzyć całkę po zmiennej . W obydwu przypadkach należy zastosować całkowanie przez części, ale po zmiennej
wystarczy jednokrotne zastosowanie wzoru na całkowanie przez części, zaś po zmiennej
należy wykonać to dwukrotnie. Zatem policzmy całkę:
Policzmy najpierw całkę:
Wstawiamy ten wynik do całki podwójnej:
Pojawiają się znowu całki liczone ze wzoru na całkowanie przez części:
U nas dla całki , gdyż
, zaś dla
, gdyż
. Wracając do całki podwójnej mamy:
Zadanie 3. Obliczyć całkę podwójną w obszarze ograniczonym przez krzywe:
1)
Rozwiązanie W tego typu zadaniu kluczowy jest poprawny rysunek obszaru Dostaliśmy w ten sposób granice całkowania. Pamiętajmy, że na zewnętrznej całce musi znaleźć się stała granica. Następna ważna rzecz: kolejność różniczek. Wewnętrzna całka odpowiada za zmianę zmiennej Najpierw całkujemy po zmiennej .
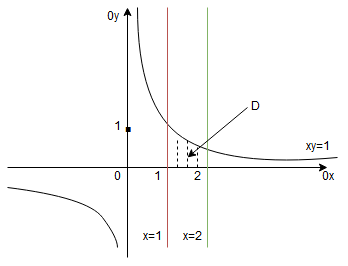 Należy teraz przeprowadzić parametryzację obszaru
Należy teraz przeprowadzić parametryzację obszaru , tzn. ustalić granice zmian zmiennych
i
. Z rysunku widzimy, że zmienna
zmienia się od 1 do 2, zaś
zaczyna się od osi
a kończy na krzywej
. Zatem obszar
zapiszemy jako:
, więc będziemy mieli
. Zatem:
(
traktujemy jak stałą).
2)
Rozwiązanie Narysujmy obszar Z rysunku widzimy, że zmienna Dostaliśmy w ten sposób granice całkowania. Pamiętajmy, że na zewnętrznej całce musi znaleźć się stała granica. Wewnętrzna całka odpowiada za zmianę zmiennej Całkujemy po zmiennej :
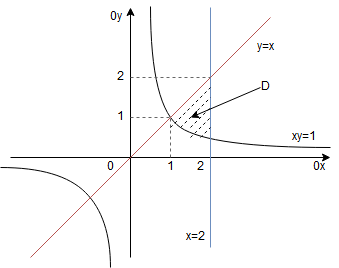
zmienia się od 1 do 2, zaś granicą dolną zmiennej
jest hiperbola (czarna)
, a granicą górną prosta (czerwona)
. Zatem obszar
zapiszemy jako:
, więc będziemy mieli
. Zatem:
(
traktujemy jak stałą).
3)
Rozwiązanie
Wykonujemy rysunek. Krzywe oraz
są to dolne ramiona tzw. paraboli z odwróconymi osiami.
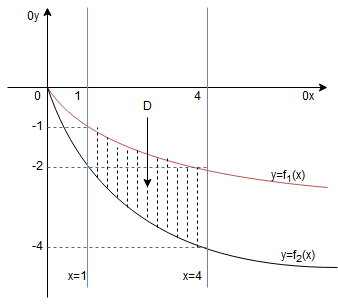
Z rysunku widzimy, że zmienna zmienia się od 1 do 4. Granicą dolną obszaru
jest czarna krzywa
, zaś górną granicą krzywa czerwona
. Zatem obszar
zapiszemy jako:
Dostaliśmy w ten sposób granice całkowania. Pamiętajmy, że na zewnętrznej całce musi znaleźć się stała granica. Wewnętrzna całka odpowiada za zmianę zmiennej , więc będziemy mieli
. Zatem:
Całkujemy po zmiennej ,
traktując jak stałą.
4)
Rozwiązanie
Wykonujemy rysunek. Przekształćmy równania prostych:
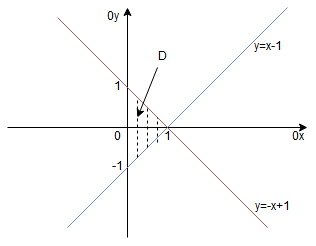
Z rysunku widzimy, że zmienna zmienia się od 0 do 1. Granicą dolną obszaru
jest niebieska prosta
, zaś granicą górna prosta czerwona
. Zatem obszar
zapiszemy jako:
Dostaliśmy w ten sposób granice całkowania. Pamiętajmy, że na zewnętrznej całce musi znaleźć się stała granica. Wewnętrzna całka odpowiada za zmianę zmiennej , więc będziemy mieli
. Zatem:
Liczymy całkę po zmiennej , zmienną
traktujemy jak stałą:
Zadanie 4. Obliczyć pole obszaru ograniczonego krzywymi:
Pole dowolnego obszaru wyraża się wzorem:
1)
Rozwiązanie Pole dowolnego obszaru Należy narysować obszar Obszar, którego pole liczymy zapisze się jako: Zatem pole wyraża się wzorem: Zatem pole obszaru wyraża się wzorem:
, którego pole mamy liczyć. Zadanie jest podobne do poprzedniego, tylko pod całką mamy zawsze liczbę 1.
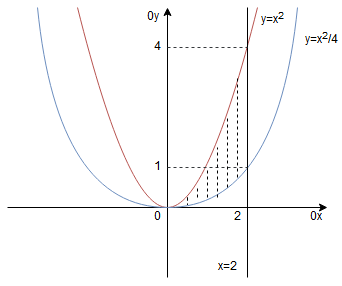
wynosi 2. Pamiętajmy, że jeśli wynik wyszedłby komuś ujemny, to jest to na pewno zła odpowiedź, gdyż liczymy pole. Zawsze warto spojrzeć na rysunek, czy mniej więcej wynik jest poprawny.
2)
Rozwiązanie Pole dowolnego obszaru Należy narysować obszar Na rysunku pominęliśmy dolne gałęzie hiperbol, aby jeszcze bardziej nie zamazywać rysunku. Nie mają one znaczenia dla zadania. Obszar Opisujemy obszary Zatem pole obszaru Liczymy oddzielnie każdą z całek. Teraz pole obszaru Zatem: Otrzymaliśmy, że pole obszaru wynosi wyraża się wzorem:
, którego pole mamy liczyć. Zadanie jest podobne do poprzedniego, tylko pod całką mamy zawsze liczbę 1.
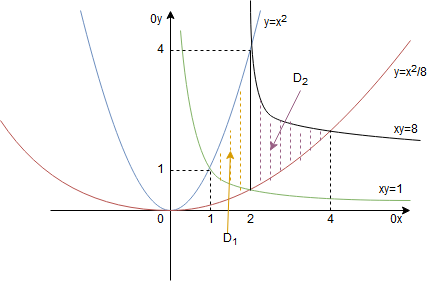
(zakreskowany w obydwu kolorach) został podzielony na dwa obszary
i
, gdyż zmienia się w nim zarówno granica dolna jak i górna. Dolna najpierw biegnie po zielonej hiperboli
, a później po czerwonej paraboli
. Granica górna początkowo biegnie po niebieskiej paraboli
, a później po czarnej hiperboli
. Mamy, że:
i
:
wynosi:
.
.
3)
Rozwiązanie
Pole dowolnego obszaru wyraża się wzorem:
Należy narysować obszar , którego pole mamy liczyć.
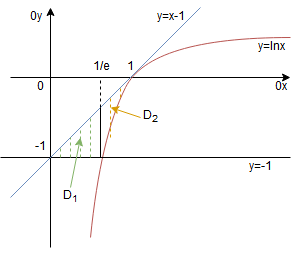
Podobnie jak w poprzednim podpunkcie dzielimy obszar na dwa obszary
i
, gdyż zmienia się granica dolna tego obszaru. Początkowo biegnie po czarnej prostej
, a później po czerwonej krzywej
. Granicą górną jest cały czas niebieska prosta
. Mamy, że:
Opisujemy obszary i
:
Zatem pole obszaru wynosi:
Liczymy oddzielnie każdą z całek.
Teraz pole obszaru .
Przy omawianiu całkowania przez części wyprowadzony był wzór na:
Zatem:
Przybliżenie podaliśmy tylko po to, aby przekonać się czy wartość wyszła dodatnia.
Liczymy pole obszaru :
Otrzymaliśmy, że pole obszaru wynosi .
4)
Rozwiązanie Pole dowolnego obszaru Należy narysować obszar Dzielimy obszar Opisujemy obszary Zatem pole obszaru Wykorzystujemy wzór: Mamy: Teraz pole obszaru Ponownie wykorzystujemy wzór: Mamy: Liczymy pole obszaru Otrzymaliśmy, że pole obszaru wynosi wyraża się wzorem:
, którego pole mamy liczyć.
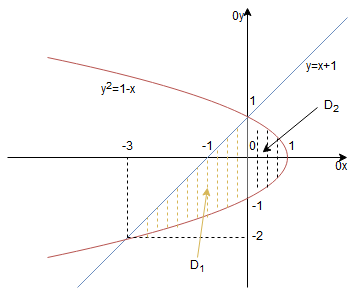
na dwa obszary
i
, gdyż zmienia się granica górna tego obszaru. Początkowo biegnie po niebieskiej prostej
, a później po czerwonej gałęzi górnej paraboli
. Granicą dolnąjest cały czas czerwona dolna gałąź paraboli
. Mamy, że:
i
:
wynosi:
Liczymy oddzielnie każdą z całek.
.
:
.