Liczby zespolone, postać trygonometryczna, teoria

Niech będzie dana liczba zespolona $\dpi{120} z=a+bi.$ Modułem liczby zespolonej $\dpi{120} z$ nazywamy liczbę rzeczywistą $\dpi{120} \sqrt{a^{2}+b^{2}}$ i oznaczamy $\dpi{120} \left | z \right |$ , czyli:

$wzór moduł liczby zespolonej$

Każdą liczbę zespoloną $\dpi{120} z=a+bi\neq 0$ możemy przedstawić w postaci:

$\dpi{120} z=\sqrt{a^{2}+b^{2}}\cdot \left ( \frac{a}{\sqrt{a^{2}+b^{2}}}+\frac{b}{\sqrt{a^{2}+b^{2}}}i \right ).$

Zauważmy, że:

$\dpi{120} \left ( \frac{a}{\sqrt{a^{2}+b^{2}}} \right )^{2}+\left ( \frac{b}{\sqrt{a^{2}+b^{2}}} \right )^{2}=\frac{a^{2}+b^{2}}{a^{2}+b^{2}}=1.$

Istnieje, więc liczba rzeczywista $\dpi{120} \varphi$ taka, że

$\dpi{120} \frac{a}{\sqrt{a^{2}+b^{2}}}=\cos \varphi ,\; \frac{b}{\sqrt{a^{2}+b^{2}}}=\sin \varphi ,$

gdyż $\dpi{120} \sin ^{2}\varphi +\cos ^{2}\varphi =1.$

Otrzymujemy stąd następującą postać liczby zespolonej $\dpi{120} z=a+bi\neq 0$

$postać trygonometryczna liczb zespolonych$

zwaną postacią trygonometryczną liczby zespolonej.

Każdą liczbę rzeczywistą $\dpi{120} \varphi$ spełniającą powyższą zależność nazywamy argumentem liczby zespolonej i oznaczamy $\dpi{120} \arg z$ . Argument nie jest określony jednoznacznie (okresowość funkcji $\dpi{120} \sin x$ i $\dpi{120} \cos x$ ), a więc również przedstawienie liczby zespolonej w postaci trygonometrycznej nie jest jednoznaczne. Wśród argumentów danej liczby zespolonej $\dpi{120} z\neq 0$ istnieje dokładnie jeden spełniający nierówność $\dpi{120} 0\leq \varphi _{0}< 2\pi .$ Nazywa się on argumentem głównym i oznaczamy go $\dpi{120} Argz.$

Moduł liczby zespolonej

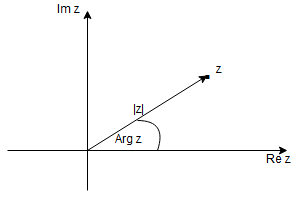
Dla danych liczb zespolonych $\dpi{120} z_{1}=\left | z_{1} \right |\cdot \left ( \cos \varphi _{1}+i\sin \varphi _{1} \right )$ oraz $\dpi{120} z_{2}=\left | z_{2} \right |\cdot \left ( \cos \varphi _{2}+i\sin \varphi _{2} \right )$ mamy:

$\dpi{120} z_{1}\cdot z_{2}=\left | z_{1} \right |\cdot \left | z_{2} \right |\left [ \left ( \cos \varphi _{1}+i\sin \varphi _{1} \right )\cdot \left ( \cos \varphi _{2}+i\sin \varphi _{2} \right ) \right ]=$

$\dpi{120} =\left | z_{1} \right |\cdot \left | z_{2} \right |\left [ \left ( \cos \varphi _{1} \cos \varphi _{2}-\sin \varphi _{1} \sin \varphi _{2} \right )+\left (\cos \varphi _{1}\sin \varphi _{2}+ \sin \varphi _{1}\cos \varphi _{2} \right ) \right ]=$

$\dpi{120} =\left | z_{1} \right |\cdot \left | z_{2} \right |\cdot \left ( \cos \left ( \varphi _{1}+\varphi _{2} \right )+i \sin \left ( \varphi _{1}+\varphi _{2} \right ) \right ).$

Wynika stąd, że:

$\dpi{120} \left | z_{1}\cdot z_{2} \right |=\left | z_{1} \right |\cdot \left | z_{2} \right |$

$\dpi{120} \arg \left ( z_{1}\cdot z_{2} \right )= \arg z_{1}+ \arg z_{2}.$

Zachodzi również analogiczna zależność dla ilorazu liczb zespolonych:

$\dpi{120} \frac{z_{1}}{z_{2}}=\frac{\left | z_{1} \right |}{\left | z_{2} \right |} \cdot \left ( \cos \left ( \varphi _{1}-\varphi _{2} \right )+i\sin \left ( \varphi _{1}-\varphi _{2} \right ) \right )$ .

Stąd:

$\dpi{120} \left | \frac{z_{1}}{z_{2}} \right |=\frac{\left | z_{1} \right |}{\left | z_{2} \right |}$

$\dpi{120} \arg \frac{z_{1}}{z_{2}}= \arg z_{1}- \arg z_{2}.$

Zapraszamy do zadań! tutaj