Ekstrema warunkowe funkcji (zadania)

W zadaniu 1 znajdujemy ekstrema warunkowe bez użycia mnożników Lagrange’a. Sprowadza się to do badania ekstremum lokalnego funkcji jednej zmiennej. W zadaniu drugim wprowadzamy mnożniki Lagrange’a. Pojawia się tzw. Hesjan obrzeżony. Jest to inna metoda znajdowania ekstremów warunkowych. Schemat badania ekstremum warunkowego znajdziemy w zakładce Wzory tutaj. Warto również zajrzeć do zakładki Teoria tutaj. Zadania kolejne to zastosowanie ekstremów warunkowych w ekonomii i geometrii.

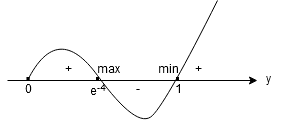
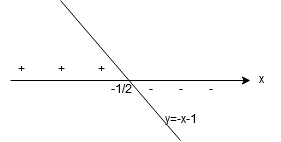
Zadanie 1. Znaleźć ekstrema funkcji $\dpi{150} \mathbf{z=f\left ( x,y \right )}$ przy warunku $\dpi{150} \mathbf{g\left ( x,y \right )=0}$ . (bez mnożników Lagrange’a)

1) $\dpi{120} f\left ( x,y \right )=x^{2}+y$ , $\dpi{120} xy-16=0$

Rozwiązanie

Funkcja $\dpi{120} g\left ( x,y \right )$ w naszym przykładzie jest równa $\dpi{120} g\left ( x,y \right )=xy-16$ . Z zależności $\dpi{120} xy-16=0$ wyliczamy zmienną $\dpi{120} y$ . Zatem:

$\dpi{120} y=\frac{16}{x}$

Wstawiamy do funkcji $\dpi{120} f\left ( x,y \right )=x^{2}+y$ i otrzymujemy funkcję jednej zmiennej $\dpi{120} x$ . Mamy:

$\dpi{120} h\left ( x \right )=f\left ( x,\frac{16}{x} \right )=x^{2}+\frac{16}{x}$

Szukamy ekstremum funkcji $\dpi{120} h\left ( x \right )$ , tak jak zwykłego ekstremum lokalnego funkcji jednej zmiennej. Warunkiem koniecznym było zerowanie się pierwszej pochodnej. Mamy:

$\dpi{120} h'\left ( x \right )=2x-\frac{16}{x^{2}}$

Przyrównujemy do zera i szukamy punktów podejrzanych o ekstremum (punktów stacjonarnych):

$\dpi{120} 2x-\frac{16}{x^{2}}=0$

$\dpi{120} 2x=\frac{16}{x^{2}}/\cdot \frac{x^{2}}{2}$

$\dpi{120} x^{3}=8$

$\dpi{120} x=2$

Jedynym punktem stacjonarnym jest punkt $\dpi{120} \left ( 2,\frac{16}{2} \right )=\left ( 2,8 \right )$ .

Warunkiem dostatecznym istnienia ekstremum lokalnego była zmiana znaku pierwszej pochodnej. Można badać go w ten sposób, ale szybszym jest zastosowanie innej wersji warunku dostatecznego wykorzystującej drugą pochodną. Jeśli $\dpi{120} x_{0}$ jest punktem stacjonarnym funkcji $\dpi{120} h\left ( x \right )$ , to w tym punkcie jest:

– minimum lokalne, gdy $\dpi{120} h''\left ( x_{0} \right )>0$ ,

– maksimum lokalne, gdy $\dpi{120} h''\left ( x_{0} \right )<0$ .

Zatem:

$\dpi{120} h''\left ( x \right )=2+\frac{32}{x^{3}}$

Wartość funkcji $\dpi{120} h''\left ( x \right )$ w punkcie $\dpi{120} x_{0}=2$ wynosi:

$\dpi{120} h''\left ( 2 \right )=2+\frac{32}{2^{3}}=6>0$ – minimum lokalne

Zatem w punkcie $\dpi{120} \left ( 2,8 \right )$ funkcja $\dpi{120} f\left ( x,y \right )=x^{2}+y$ osiąga minimum przy warunku $\dpi{120} xy-16=0$ . Jest ono równe:

$\dpi{120} f_{min}\left ( 2,8 \right )=2^{2}+8=12$

Pokaż rozwiązanie

Zwiń

2) $\dpi{120} f\left ( x,y \right )=4-x^{2}-y^{2}$ , $\dpi{120} y-x^{2}+\frac{3}{2}=0$ ,

Rozwiązanie

Z zależności $\dpi{120} y-x^{2}+\frac{3}{2}=0$ wyliczamy zmienną $\dpi{120} y$ . Zatem:

$\dpi{120} y=x^{2}-\frac{3}{2}$

Wstawiamy do funkcji $\dpi{120} f\left ( x,y \right )=4-x^{2}-y^{2}$ i otrzymujemy funkcję jednej zmiennej $\dpi{120} x$ . Mamy:

$\dpi{120} h\left ( x \right )=f\left ( x,x^{2} -\frac{3}{2}\right )=4-x^{2}-\left ( x^{2} -\frac{3}{2}\right )^{2}=4-x^{4}+2x^{2}-\frac{9}{4}$

$\dpi{120} h\left ( x \right )=-x^{4}+2x^{2}+\frac{7}{4}$

Szukamy ekstremum funkcji $\dpi{120} h\left ( x \right )$ . Warunkiem koniecznym jest zerowanie się pierwszej pochodnej. Mamy:

$\dpi{120} h'\left ( x \right )=-4x^{3}+4x$

Przyrównujemy do zera i szukamy punktów podejrzanych o ekstremum (punktów stacjonarnych):

$\dpi{120} -4x^{3}+4x=0/:4$

$\dpi{120} -x^{3}+x=0$

$\dpi{120} x\left (-x^{2}+1 \right )=0$

$\dpi{120} x=0,\; \; \; x=-1,\; \;\; x=1$

Punktami stacjonarnymi są punkty $\dpi{120} A=\left ( 0,0^{2}-\frac{3}{2} \right )=\left ( 0,-\frac{3}{2} \right )$ , $\dpi{120} B=\left ( -1,\left ( -1 \right )^{2}-\frac{3}{2} \right )=\left ( -1,-\frac{1}{2} \right )$ ,

$\dpi{120} C=\left ( 1,\1 ^{2}-\frac{3}{2} \right )=\left ( 1,-\frac{1}{2} \right )$ .

Badamy warunek dostateczny istnienia ekstremum. Zatem:

$\dpi{120} h''\left ( x \right )=-12x^{2}+4$

Liczymy wartości funkcji $\dpi{120} h''\left ( x \right )$ w punktach $\dpi{120} x_{1}=0,\: x_{2}=-1,\: x_{3}=1$ :

$\dpi{120} h''\left ( 0 \right )=-12\cdot 0^{2}+4=4>0$ – minimum lokalne

$\dpi{120} h''\left ( -1 \right )=-12\cdot \left ( -1 \right )^{2}+4=-8<0$ – maksimum lokalne

$\dpi{120} h''\left ( 1 \right )=-12\cdot 1 ^{2}+4=-8<0$ – maksimum lokalne

Zatem ekstrema warunkowe funkcji $\dpi{120} f\left ( x,y \right )=4-x^{2}-y^{2}$ wynoszą:

$\dpi{120} f_{min}\left ( 0,-\frac{3}{2} \right )=4-0^{2}-\left ( -\frac{3}{2} \right )^{2}=\frac{7}{4}$

$\dpi{120} f_{max}\left ( -1,-\frac{1}{2} \right )=4-\left ( -1 \right )^{2}-\left ( -\frac{1}{2} \right )^{2}=\frac{11}{4}$

$\dpi{120} f_{max}\left ( 1,-\frac{1}{2} \right )=4-1 ^{2}-\left ( -\frac{1}{2} \right )^{2}=\frac{11}{4}$

Pokaż rozwiązanie

Zwiń

3) $\dpi{120} f\left ( x,y \right )=x^{2}y$ , $\dpi{120} x-\ln ^{2}y=0$

Rozwiązanie

Dziedziną naszej funkcji jest $\dpi{120} D:\left \{ \left ( x,y \right ):x\in \mathbb{R},y>0 \right \}$ .

Z zależności $\dpi{120} x-\ln ^{2}y=0$ wyliczamy zmienną $\dpi{120} x$ . Zatem:

$\dpi{120} x=\ln ^{2}y$

Wstawiamy do funkcji $\dpi{120} f\left ( x,y \right )=x^{2}y$ i otrzymujemy funkcję jednej zmiennej $\dpi{120} y$ . Mamy:

$\dpi{120} h\left ( y \right )=f\left ( \ln ^{2}y,y\right )=\left ( \ln ^{2}y \right )^{2}\cdot y=y \ln ^{4}y$

Szukamy ekstremum funkcji $\dpi{120} h\left ( y \right )$ . Warunkiem koniecznym jest zerowanie się pierwszej pochodnej. Mamy:

$\dpi{120} h'\left ( y \right )=\ln ^{4}y+y\cdot 4 \ln ^{3}y\cdot \frac{1}{y}$

$\dpi{120} h'\left ( y \right )=\ln ^{4}y+4 \ln ^{3}y$

$\dpi{120} h'\left ( y \right )=\ln ^{3}y\cdot \left ( \ln y+4 \right )$

Przyrównujemy do zera i szukamy punktów podejrzanych o ekstremum (punktów stacjonarnych):

$\dpi{120} \ln ^{3}y\cdot \left ( \ln y+4 \right )=0$

$\dpi{120} \ln ^{3}y=0\; \; \vee \; \; \ln y+4=0$

$\dpi{120} \ln y=0\; \; \; \vee \; \; \; \ln y=-4$

$\dpi{120} y=1\; \; \; \; \; \vee\; \; \;\; \; y=e^{-4}$

Punktami stacjonarnymi są punkty:

$\dpi{120} A=\left ( \ln ^{2}1,1 \right )=\left ( 0,1 )$ ,

$\dpi{120} B=\left ( \ln ^{2}\left (e^{-4} \right ),e^{-4} \right )=\left ( \left (-4 \right )^{2},e^{-4} \right )=\left ( 16,e^{-4} \right )$ .

Badamy znak pochodnej w punktach $\dpi{120} y_{1}=1,\: y_{2}=e^{-4}$ . Mamy:

$\dpi{120} \ln ^{3}y>0\Leftrightarrow y>1$

$\dpi{120} \ln y+4>0\Leftrightarrow y>e^{-4}$

Zatem:

Zatem ekstrema warunkowe funkcji $\dpi{120} f\left ( x,y \right )=x^{2}y$ przy warunku $\dpi{120} x-\ln ^{2}y=0$ wynoszą:

$\dpi{120} f_{min}\left ( 0,1\right )=0^{2}\cdot 1=0$

$\dpi{120} f_{max}\left ( 16,e^{-4}\right )=16^{2}\cdot e^{-4}=\frac{16^{2}}{e^{4}}$

Pokaż rozwiązanie

Zwiń

Zadanie 2. Znaleźć ekstrema funkcji $\dpi{150} z=f\left ( x,y \right )$ przy warunku $\dpi{150} g\left ( x,y \right )=0$ . (mnożniki Lagrange’a zob. tutaj )

1) $\dpi{120} f\left ( x,y \right )=x^{2}+y$ , $\dpi{120} xy-16=0$

Rozwiązanie

Przykład ten był rozwiązany wcześniej bez mnożników Lagrange’a. Teraz wprowadzimy mnożniki Lagrange’a. Funkcja $\dpi{120} g\left ( x,y \right )$ ma postać $\dpi{120} g\left ( x,y \right )=xy-16$ . Tworzymy funkcję $\dpi{120} L\left ( x,y,\lambda \right )$ :

$\dpi{120} L\left ( x,y,\lambda \right )=f\left ( x,y \right )+\lambda \cdot g\left ( x,y \right )$

$\dpi{120} L\left ( x,y,\lambda \right )=x^{2}+y+\lambda \cdot \left ( xy-16 \right )$

Warunek konieczny

Liczymy pochodne cząstkowe:

$\dpi{120} L'_{x}=2x+\lambda y$

$\dpi{120} L'_{y}=1+\lambda x$

$\dpi{120} L'_{\lambda }=xy-16$

Przyrównujemy pochodne cząstkowe do zera:

$\dpi{120} \left\{\begin{matrix} 2x+\lambda y=0\\ 1+\lambda x=0\; \; \\ xy-16=0 \end{matrix}\right.$

Rozwiązujemy układ równań dowolną metodą, np. metodą podstawienia. Z drugiego równania wyznaczamy $\dpi{120} \lambda =-\frac{1}{x}$ i wstawiamy do pozostałych równań:

$\dpi{120} \left\{\begin{matrix} \lambda =-\frac{1}{x}\; \;\; \; \; \; \; \; \; \; \; \; \; \; \; \\ 2x-\frac{1}{x}\cdot y=0/\cdot x\\ xy-16=0\; \;\; \; \; \; \; \; \end{matrix}\right.$

$\dpi{120} \left\{\begin{matrix} \lambda =-\frac{1}{x}\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \\ 2x^{2}-y=0\Rightarrow y=2x^{2}\\ xy-16=0 \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \end{matrix}\right.$

$\dpi{120} \left\{\begin{matrix} \lambda =-\frac{1}{x} \; \; \; \; \;\; \; \; \; \; \; \; \; \; \; \; \; \; \\ y=2x^{2}\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \\ x\cdot 2x^{2}-16=0/:2 \end{matrix}\right.$

$\dpi{120} \left\{\begin{matrix} \lambda =-\frac{1}{x} \; \;\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \\ y=2x^{2} \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \\ x^{3}-8=0\Rightarrow x=2\end{matrix}\right.$

$\dpi{120} \left\{\begin{matrix} \lambda =-\frac{1}{2}\\ y=8\; \; \\ x=2\; \; \end{matrix}\right.$

Mamy jeden punkt stacjonarny $\dpi{120} \left ( x,y,\lambda \right )=\left ( 2,8,-\frac{1}{2} \right )$ .

Warunek dostateczny

Badamy znak tzw. Hesjanu obrzeżonego:

$\dpi{120} \left |\bar{H } \right |=\begin{vmatrix} 0 & g'_{x} & g'_{y}\\ g'_{x}& L''_{xx}& L''_{xy}\\ g'_{y}&L''_{yx} & L''_{yy} \end{vmatrix}.$

Liczymy potrzebne pochodne cząstkowe:

$\dpi{120} g'_{x}=y$ , $\dpi{120} g'_{y}=x$

$\dpi{120} L''_{xx}=2$ , $\dpi{120} L''_{xy}=\lambda$

$\dpi{120} L''_{yx}=\lambda$ , $\dpi{120} L''_{yy}=0$

Liczymy wartości tych pochodnych w punkcie stacjonarnym $\dpi{120} \left ( x,y,\lambda \right )=\left ( 2,8,-\frac{1}{2} \right )$ :

$\dpi{120} g'_{x}=8$ , $\dpi{120} g'_{y}=2$

$\dpi{120} L''_{xx}=2$ , $\dpi{120} L''_{xy}=-\frac{1}{2}$

$\dpi{120} L''_{yx}=-\frac{1}{2}$ , $\dpi{120} L''_{yy}=0$

Wstawiamy do Hesjanu obrzeżonego:

$\dpi{120} \left |\bar{H } \right |=\begin{vmatrix} 0 & 8 & 2\\ 8& 2& -\frac{1}{2}\\ 2&-\frac{1}{2} & 0 \end{vmatrix}\begin{matrix} 0 & 8\\ 8 & 2\\ 2& -\frac{1}{2} \end{matrix}=-8-8-8=-24<0$

Ponieważ wartość Hesjanu obrzeżonego jest ujemna, zatem w punkcie $\dpi{120} \left ( 2,8 \right )$ funkcja $\dpi{120} f\left ( x,y \right )=x^{2}+y$ osiąga minimum warunkowe przy warunku $\dpi{120} xy-16=0$ . Jest ono równe:

$\dpi{120} f_{min}\left ( 2,8 \right )=2^{2}+8=12$

Pokaż rozwiązanie

Zwiń

2) $\dpi{120} f\left ( x,y \right )=x^{2}+y^{2}$ , $\dpi{120} x+4y-2=0$

Rozwiązanie

Funkcja $\dpi{120} g\left ( x,y \right )$ ma postać $\dpi{120} g\left ( x,y \right )=x+4y-2$ . Tworzymy funkcję $\dpi{120} L\left ( x,y,\lambda \right )$ :

$\dpi{120} L\left ( x,y,\lambda \right )=f\left ( x,y \right )+\lambda \cdot g\left ( x,y \right )$

$\dpi{120} L\left ( x,y,\lambda \right )=x^{2}+y^{2}+\lambda \cdot \left ( x+4y-2 \right )$

Warunek konieczny

Liczymy pochodne cząstkowe:

$\dpi{120} L'_{x}=2x+\lambda$

$\dpi{120} L'_{y}=2y+4\lambda$

$\dpi{120} L'_{\lambda }=x+4y-2$

Przyrównujemy pochodne cząstkowe do zera:

$\dpi{120} \left\{\begin{matrix} 2x+\lambda =0\; \; \; \; \; \; \; \\ 2y+4\lambda =0\; \;\; \; \; \\ x+4y-2=0 \end{matrix}\right.$

Rozwiązujemy układ równań dowolną metodą, np. metodą podstawienia. Z pierwszego równania wyznaczamy $\dpi{120} \lambda =-2x$ i wstawiamy do pozostałych równań:

$\dpi{120} \left\{\begin{matrix} \lambda =-2x\; \; \; \; \;\; \; \; \; \; \; \; \; \; \\ 2y+4\cdot \left ( -2x \right )=0\\ x+4y-2=0\; \; \; \; \; \; \end{matrix}\right.$

$\dpi{120} \left\{\begin{matrix} \lambda =-2x\; \; \; \; \; \; \; \; \; \; \; \; \;\; \; \; \; \; \; \; \\ 2y-8x=0\Rightarrow y=4x\\ x+4y-2=0 \; \; \; \; \; \; \; \; \; \; \; \end{matrix}\right.$

$\dpi{120} \left\{\begin{matrix} \lambda =-2x \; \; \; \; \; \; \;\; \; \; \; \; \; \; \\ y=4x\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \\ x+4\cdot 4x-2=0 \end{matrix}\right.$

$\dpi{120} \left\{\begin{matrix} \lambda =-2x \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \\ y=4x\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \\ 17x-2=0\Rightarrow x=\frac{2}{17} \end{matrix}\right.$

$\dpi{120} \left\{\begin{matrix} \lambda =-\frac{4}{17}\\ y=\frac{8}{17}\; \; \\ x=\frac{2}{17}\; \; \end{matrix}\right.$

Mamy jeden punkt stacjonarny $\dpi{120} \left ( x,y,\lambda \right )=\left ( \frac{2}{17},\frac{8}{17},-\frac{4}{17} \right )$ .

Warunek dostateczny

Badamy znak tzw. Hesjanu obrzeżonego:

$\dpi{120} \left |\bar{H } \right |=\begin{vmatrix} 0 & g'_{x} & g'_{y}\\ g'_{x}& L''_{xx}& L''_{xy}\\ g'_{y}&L''_{yx} & L''_{yy} \end{vmatrix}.$

Liczymy potrzebne pochodne cząstkowe:

$\dpi{120} g'_{x}=1$ , $\dpi{120} g'_{y}=4$

$\dpi{120} L''_{xx}=2$ , $\dpi{120} L''_{xy}=0$

$\dpi{120} L''_{yx}=0$ , $\dpi{120} L''_{yy}=2$

Wartości pochodnych są stałe, więc wstawiamy je do Hesjanu obrzeżonego:

$\dpi{120} \left |\bar{H } \right |=\begin{vmatrix} 0 & 1 & 4\\ 1& 2& 0\\ 4&0 & 2 \end{vmatrix}\begin{matrix} 0 & 1\\ 1 & 2\\ 4& 0 \end{matrix}=-32-2=-34<0$

Ponieważ wartość Hesjanu obrzeżonego jest ujemna, zatem w punkcie $\dpi{120} \left ( \frac{2}{17},\frac{8}{17} \right )$ funkcja $\dpi{120} f\left ( x,y \right )=x^{2}+y^{2}$ osiąga minimum warunkowe przy warunku $\dpi{120} x+4y-2=0$ . Jest ono równe:

$\dpi{120} f_{min}\left ( \frac{2}{17},\frac{8}{17} \right )=\left ( \frac{2}{17} \right )^{2}+\left ( \frac{8}{17} \right )^{2}=\frac{68}{17}$

Pokaż rozwiązanie

Zwiń

3) $\dpi{120} f\left ( x,y \right )=xy+x+y$ , $\dpi{120} x+2y-3=0$

Rozwiązanie

Funkcja $\dpi{120} g\left ( x,y \right )$ ma postać $\dpi{120} g\left ( x,y \right )=x+2y-3$ . Tworzymy funkcję $\dpi{120} L\left ( x,y,\lambda \right )$ :

$\dpi{120} L\left ( x,y,\lambda \right )=f\left ( x,y \right )+\lambda \cdot g\left ( x,y \right )$

$\dpi{120} L\left ( x,y,\lambda \right )=xy+x+y+\lambda \cdot \left ( x+2y-3 \right )$

Warunek konieczny

Liczymy pochodne cząstkowe:

$\dpi{120} L'_{x}=y+1+\lambda$

$\dpi{120} L'_{y}=x+1+2\lambda$

$\dpi{120} L'_{\lambda }=x+2y-3$

Przyrównujemy pochodne cząstkowe do zera:

$\dpi{120} \left\{\begin{matrix} y+1+\lambda =0\; \; \\ x+1+2\lambda =0 \\ x+2y-3=0 \end{matrix}\right.$

Rozwiązujemy układ równań dowolną metodą, np. metodą podstawienia. Z pierwszego równania wyznaczamy $\dpi{120} \lambda =-y-1$ i wstawiamy do pozostałych równań:

$\dpi{120} \left\{\begin{matrix} \lambda =-y-1\; \; \; \; \;\; \; \; \; \; \;\; \; \; \; \; \; \; \; \\ x+1+2\cdot \left ( -y-1 \right ) =0\\ x+2y-3=0\; \; \; \; \; \;\; \; \; \; \; \; \; \; \end{matrix}\right.$

$\dpi{120} \left\{\begin{matrix} \lambda =-y-1\; \; \; \; \; \\ x-2y-1 =0\\ x+2y-3=0 \end{matrix}\right.$

Dodajmy stronami drugie i trzecie równanie:

$\dpi{120} \left\{\begin{matrix} \lambda =-y-1\; \; \; \; \; \; \; \; \; \; \; \; \: \\ 2x-4=0\Rightarrow x=2 \end{matrix}\right.$

Wstawiając otrzymujemy:

$\dpi{120} \left\{\begin{matrix} \lambda =-\frac{3}{2}\\ y=\frac{1}{2}\; \; \\ x=2\; \; \end{matrix}\right.$

Mamy jeden punkt stacjonarny $\dpi{120} \left ( x,y,\lambda \right )=\left ( 2,\frac{1}{2},-\frac{3}{2} \right )$ .

Warunek dostateczny

Badamy znak tzw. Hesjanu obrzeżonego:

$\dpi{120} \left |\bar{H } \right |=\begin{vmatrix} 0 & g'_{x} & g'_{y}\\ g'_{x}& L''_{xx}& L''_{xy}\\ g'_{y}&L''_{yx} & L''_{yy} \end{vmatrix}.$

Liczymy potrzebne pochodne cząstkowe:

$\dpi{120} g'_{x}=1$ , $\dpi{120} g'_{y}=2$

$\dpi{120} L''_{xx}=0$ , $\dpi{120} L''_{xy}=1$

$\dpi{120} L''_{yx}=1$ , $\dpi{120} L''_{yy}=0$

Wartości pochodnych są stałe, więc wstawiamy je do Hesjanu obrzeżonego:

$\dpi{120} \left |\bar{H } \right |=\begin{vmatrix} 0 & 1 & 2\\ 1& 0& 1\\ 2&1 & 0 \end{vmatrix}\begin{matrix} 0 & 1\\ 1 & 0\\ 2& 1 \end{matrix}=2+2=4>0$

Ponieważ wartość Hesjanu obrzeżonego jest dodatnia, zatem w punkcie $\dpi{120} \left ( 2,\frac{1}{2} \right )$ funkcja $\dpi{120} f\left ( x,y \right )=xy+x+y$ osiąga maksimum warunkowe przy warunku $\dpi{120} x+2y-3=0$ . Jest ono równe:

$\dpi{120} f_{max}\left ( 2,\frac{1}{2} \right )=2\cdot \frac{1}{2}+2+\frac{1}{2}=\frac{7}{2}$

Pokaż rozwiązanie

Zwiń

4) $\dpi{120} f\left ( x,y \right )=x^{2}-y^{2}$ , $\dpi{120} x^{2}+y^{2}=1$ dłuższy i trudniejszy

Rozwiązanie

Funkcja $\dpi{120} g\left ( x,y \right )$ ma postać $\dpi{120} g\left ( x,y \right )=x^{2}+y^{2}-1$ . Tworzymy funkcję $\dpi{120} L\left ( x,y,\lambda \right )$ :

$\dpi{120} L\left ( x,y,\lambda \right )=f\left ( x,y \right )+\lambda \cdot g\left ( x,y \right )$

$\dpi{120} L\left ( x,y,\lambda \right )=x^{2}-y^{2}+\lambda \cdot \left ( x^{2}+y^{2}-1 \right )$

Warunek konieczny

Liczymy pochodne cząstkowe:

$\dpi{120} L'_{x}=2x+2\lambda\, x$

$\dpi{120} L'_{y}=-2y+2\lambda\, y$

$\dpi{120} L'_{\lambda }=x^{2}+y^{2}-1$

Przyrównujemy pochodne cząstkowe do zera:

$\dpi{120} \left\{\begin{matrix} 2x+2\lambda\, x =0\Rightarrow 2x\cdot \left ( 1+\lambda \right )=0\; \; \\ -2y+2\lambda\, y =0 \Rightarrow 2y\cdot \left ( -1+\lambda \right )=0\\ x^{2}+y^{2}-1=0 \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \end{matrix}\right.$

Aby układ miał rozwiązanie mamy $\dpi{120} x=0$ lub $\dpi{120} y=0$ . (Uważajmy, aby nie dzielić równania pierwszego przez $\dpi{120} x$ , a drugiego przez $\dpi{120} y$ ponieważ w ten sposób tracimy rozwiązania.)

Przypadek 1

Dla $\dpi{120} x=0$ .

Wstawiamy do trzeciego równania i otrzymujemy:

$\dpi{120} 0^{2}+y^{2}-1=0$

$\dpi{120} \left ( y-1 \right )\left ( y+1 \right )=0$

$\dpi{120} y=-1\; \; \vee \; \; y=1$

Wstawiając $\dpi{120} y=-1$ oraz $\dpi{120} y=1$ do równania drugiego mamy:

$\dpi{120} 2\cdot \left ( -1 \right )\cdot \left ( -1+\lambda \right )=0$ oraz $\dpi{120} 2\cdot 1\cdot \left ( -1+\lambda \right )=0$

Stąd w obydwu przypadkach dostajemy:

$\dpi{120} \lambda =1$

Otrzymujemy dwa pierwsze punkty stacjonarne $\dpi{120} A=\left ( 0,-1 ,1\right )$ , $\dpi{120} B=\left ( 0,1 ,1\right )$ .

Przypadek 2

Dla $\dpi{120} y=0$ .

Wstawiamy do trzeciego równania i otrzymujemy:

$\dpi{120} x^{2}+0^{2}-1=0$

$\dpi{120} \left ( x-1 \right )\left ( x+1 \right )=0$

$\dpi{120} x=-1\; \; \vee \; \; x=1$

Wstawiając $\dpi{120} x=-1$ oraz $\dpi{120} x=1$ do równania pierwszego mamy:

$\dpi{120} 2\cdot \left ( -1 \right )\cdot \left ( 1+\lambda \right )=0$ oraz $\dpi{120} 2\cdot 1\cdot \left ( 1+\lambda \right )=0$

Stąd w obydwu przypadkach dostajemy:

$\dpi{120} \lambda =-1$

Otrzymujemy dwa kolejne punkty stacjonarne $\dpi{120} C=\left ( -1,0 ,-1\right )$ , $\dpi{120} D=\left ( 1,0 ,-1\right )$ .

Warunek dostateczny

Badamy znak tzw. Hesjanu obrzeżonego:

$\dpi{120} \left |\bar{H } \right |=\begin{vmatrix} 0 & g'_{x} & g'_{y}\\ g'_{x}& L''_{xx}& L''_{xy}\\ g'_{y}&L''_{yx} & L''_{yy} \end{vmatrix}.$

Liczymy potrzebne pochodne cząstkowe:

$\dpi{120} g'_{x}=2x$ , $\dpi{120} g'_{y}=2y$

$\dpi{120} L''_{xx}=2+2\lambda$ , $\dpi{120} L''_{xy}=0$

$\dpi{120} L''_{yx}=0$ , $\dpi{120} L''_{yy}=-2+2\lambda$

Rozpatrzmy 4 możliwości ze względu na 4 punkty stacjonarne.

1. Dla punktu $\dpi{120} A=\left ( 0,-1 ,1\right )$ mamy:

$\dpi{120} g'_{x}=2\cdot 0=0$ , $\dpi{120} g'_{y}=2\cdot \left ( -1 \right )=-2$

$\dpi{120} L''_{xx}=2+2\cdot 1=4$ , $\dpi{120} L''_{xy}=0$

$\dpi{120} L''_{yx}=0$ , $\dpi{120} L''_{yy}=-2+2\cdot 1=0$

Zatem Hesjan obrzeżony wynosi:

$\dpi{120} \left |\bar{H } \right |=\begin{vmatrix} 0 & 0 & -2\\ 0& 4& 0\\ -2&0 & 0 \end{vmatrix}\begin{matrix} 0 & 0\\ 0 & 4\\ -2& 0 \end{matrix}=-16<0$

Ponieważ wartość Hesjanu obrzeżonego jest ujemna, zatem w punkcie $\dpi{120} \left ( 0,-1 \right )$ funkcja $\dpi{120} f\left ( x,y \right )=x^{2}-y^{2}$ osiąga minimum warunkowe przy warunku $\dpi{120} x^{2}+y^{2}-1=0$ . Jest ono równe:

$\dpi{120} f_{min}\left ( 0,-1 \right )=0^{2}-\left ( -1 \right )^{2}=-1$

2. Dla punktu $\dpi{120} B=\left ( 0,1 ,1\right )$ mamy:

$\dpi{120} g'_{x}=2\cdot 0=0$ , $\dpi{120} g'_{y}=2\cdot 1=2$

$\dpi{120} L''_{xx}=2+2\cdot 1=4$ , $\dpi{120} L''_{xy}=0$

$\dpi{120} L''_{yx}=0$ , $\dpi{120} L''_{yy}=-2+2\cdot 1=0$

Zatem Hesjan obrzeżony wynosi:

$\dpi{120} \left |\bar{H } \right |=\begin{vmatrix} 0 & 0 & 2\\ 0& 4& 0\\ 2&0 & 0 \end{vmatrix}\begin{matrix} 0 & 0\\ 0 & 4\\ 2& 0 \end{matrix}=-16<0$

Ponieważ wartość Hesjanu obrzeżonego jest ujemna, zatem w punkcie $\dpi{120} \left ( 0,1 \right )$ funkcja $\dpi{120} f\left ( x,y \right )=x^{2}-y^{2}$ osiąga minimum warunkowe przy warunku $\dpi{120} x^{2}+y^{2}-1=0$ . Jest ono równe:

$\dpi{120} f_{min}\left ( 0,1 \right )=0^{2}-1 ^{2}=-1$

3. Dla punktu $\dpi{120} C=\left ( -1,0 ,-1\right )$ mamy:

$\dpi{120} g'_{x}=2\cdot \left ( -1 \right )=-2$ , $\dpi{120} g'_{y}=2\cdot 0=0$

$\dpi{120} L''_{xx}=2+2\cdot \left (-1 \right )=0$ , $\dpi{120} L''_{xy}=0$

$\dpi{120} L''_{yx}=0$ , $\dpi{120} L''_{yy}=-2+2\cdot \left (-1 \right )=-4$

Zatem Hesjan obrzeżony wynosi:

$\dpi{120} \left |\bar{H } \right |=\begin{vmatrix} 0 & -2 & 0\\ -2& 0& 0\\ 0&0 & -4 \end{vmatrix}\begin{matrix} 0 & -2\\ -2 & 0\\ 0& 0 \end{matrix}=16>0$

Ponieważ wartość Hesjanu obrzeżonego jest dodatnia, zatem w punkcie $\dpi{120} \left ( -1,0 \right )$ funkcja $\dpi{120} f\left ( x,y \right )=x^{2}-y^{2}$ osiąga maksimum warunkowe przy warunku $\dpi{120} x^{2}+y^{2}-1=0$ . Jest ono równe:

$\dpi{120} f_{max}\left ( -1,0 \right )=\left ( -1 \right )^{2}-0^{2}=1$

4. Dla punktu $\dpi{120} D=\left ( 1,0 ,-1\right )$ mamy:

$\dpi{120} g'_{x}=2\cdot 1=2$ , $\dpi{120} g'_{y}=2\cdot 0=0$

$\dpi{120} L''_{xx}=2+2\cdot \left (-1 \right )=0$ , $\dpi{120} L''_{xy}=0$

$\dpi{120} L''_{yx}=0$ , $\dpi{120} L''_{yy}=-2+2\cdot \left (-1 \right )=-4$

Zatem Hesjan obrzeżony wynosi:

$\dpi{120} \left |\bar{H } \right |=\begin{vmatrix} 0 & 2 & 0\\ 2& 0& 0\\ 0&0 & -4 \end{vmatrix}\begin{matrix} 0 & 2\\ 2 & 0\\ 0& 0 \end{matrix}=16>0$

Ponieważ wartość Hesjanu obrzeżonego jest dodatnia, zatem w punkcie $\dpi{120} \left ( 1,0 \right )$ funkcja $\dpi{120} f\left ( x,y \right )=x^{2}-y^{2}$ osiąga maksimum warunkowe przy warunku $\dpi{120} x^{2}+y^{2}-1=0$ . Jest ono równe:

$\dpi{120} f_{max}\left ( 1,0 \right )=1 ^{2}-0^{2}=1$

Podsumowując mamy w punkcie:

1. $\dpi{120} \left ( 0,-1 \right )$ minimum warunkowe równe $\dpi{120} f_{min}\left ( 0,-1 \right )=-1$ ,

2. $\dpi{120} \left ( 0,1 \right )$ minimum warunkowe równe $\dpi{120} f_{min}\left ( 0,1 \right )=-1$ ,

3. $\dpi{120} \left ( -1,0 \right )$ maksimum warunkowe równe $\dpi{120} f_{max}\left ( -1,0 \right )=1$ ,

4. $\dpi{120} \left ( 1,0 \right )$ maksimum warunkowe równe $\dpi{120} f_{max}\left ( 1,0 \right )=1$ .

Pokaż rozwiązanie

Zwiń

Zadanie 3. Rozważmy konsumenta, dla którego użyteczność z koszyka dwu towarów $\dpi{150} \mathbf{x,y}$ jest dana wzorem $\dpi{150} \mathbf{u\left ( x,y \right )=xy}$ . Wiemy, że jednostka towaru $\dpi{150} \mathbf{x}$ kosztuje 4 zł, a jednostka towaru $\dpi{150} \mathbf{y}$ kosztuje 1 zł. Załóżmy, że konsument ma do wydania na te towary 16 zł. Ile jednostek pierwszego, a ile drugiego towaru powinien kupić, by zmaksymalizować użyteczność koszyka tych dóbr?

Rozwiązanie

W tym zadaniu naszą funkcją $\dpi{120} f\left ( x,y \right )$ jest funkcja użyteczności $\dpi{120} u\left ( x,y \right )=xy$ , zaś funkcja $\dpi{120} g\left ( x,y \right )$ jest równa $\dpi{120} g\left ( x,y \right )=4x+y-16$ (mamy 16 zł na towar x za 4 zł i towar y za 1 zł, czyli 4x+1y=16)

Tworzymy funkcję $\dpi{120} L\left ( x,y,\lambda \right )$ :

$\dpi{120} L\left ( x,y,\lambda \right )=u\left ( x,y \right )+\lambda \cdot g\left ( x,y \right )$

$\dpi{120} L\left ( x,y,\lambda \right )=xy+\lambda \cdot \left ( 4x+y-16 \right )$

Warunek konieczny

Liczymy pochodne cząstkowe:

$\dpi{120} L'_{x}=y+4\lambda$

$\dpi{120} L'_{y}=x+\lambda$

$\dpi{120} L'_{\lambda }=4x+y-16$

Przyrównujemy pochodne cząstkowe do zera:

$\dpi{120} \left\{\begin{matrix} y+4\lambda =0\; \; \; \; \; \; \; \\ x+\lambda =0 \; \; \; \; \; \; \; \; \; \\ 4x+y-12=0 \end{matrix}\right.$

Rozwiązujemy układ równań dowolną metodą, np. metodą podstawienia. Z drugiego równania wyznaczamy $\dpi{120} \lambda =-x$ i wstawiamy do pozostałych równań:

$\dpi{120} \left\{\begin{matrix} \lambda =-x\; \; \; \; \;\; \; \; \; \; \;\; \; \\ y-4x =0\; \; \; \; \; \; \; \; \\ 4x+y-16=0\end{matrix}\right.$

Dodajmy stronami drugie i trzecie równanie:

$\dpi{120} \left\{\begin{matrix} \lambda =-x\; \; \; \; \; \; \; \; \; \; \; \; \: \; \; \; \; \; \; \\ 2y-16=0\Rightarrow y=8 \end{matrix}\right.$

Wstawiając otrzymujemy:

$\dpi{120} \left\{\begin{matrix} \lambda =-2\\ x=2\; \; \\ y=8\; \; \end{matrix}\right.$

Mamy jeden punkt stacjonarny $\dpi{120} \left ( x,y,\lambda \right )=\left (2,8,-2 \right )$ .

Warunek dostateczny

Badamy znak tzw. Hesjanu obrzeżonego:

$\dpi{120} \left |\bar{H } \right |=\begin{vmatrix} 0 & g'_{x} & g'_{y}\\ g'_{x}& L''_{xx}& L''_{xy}\\ g'_{y}&L''_{yx} & L''_{yy} \end{vmatrix}.$

Liczymy potrzebne pochodne cząstkowe:

$\dpi{120} g'_{x}=4$ , $\dpi{120} g'_{y}=1$

$\dpi{120} L''_{xx}=0$ , $\dpi{120} L''_{xy}=1$

$\dpi{120} L''_{yx}=1$ , $\dpi{120} L''_{yy}=0$

Wartości pochodnych są stałe, więc wstawiamy je do Hesjanu obrzeżonego:

$\dpi{120} \left |\bar{H } \right |=\begin{vmatrix} 0 & 4 & 1\\ 4& 0& 1\\ 1&1 & 0 \end{vmatrix}\begin{matrix} 0 & 4\\ 4 & 0\\ 1& 1 \end{matrix}=4+4=8>0$

Ponieważ wartość Hesjanu obrzeżonego jest dodatnia, zatem w punkcie $\dpi{120} \left ( 2,8 \right )$ funkcja $\dpi{120} f\left ( x,y \right )=xy$ osiąga maksimum warunkowe przy warunku $\dpi{120} 4x+y-16=0$ . Powinniśmy zatem kupić 2 sztuki towaru $\dpi{120} x$ oraz 8 sztuk towaru $\dpi{120} y$ .

Pokaż rozwiązanie

Zwiń

Zadanie 4. Konsument może wydać 1280 zł na dwa dobra $\dpi{150} \mathbf{x}$ i $\dpi{150} \mathbf{y}$ , kosztujące odpowiednio 12 zł i 16 zł za jednostkę. Jego funkcja użyteczności dana jest wzorem $\dpi{150} \mathbf{u\left ( x,y \right )=x^{\frac{3}{4}}\cdot y^{\frac{1}{4}}}$ .Wyznacz wartości $\dpi{150} \mathbf{x}$ i $\dpi{150} \mathbf{y}$ maksymalizujące użyteczność $\dpi{150} \mathbf{u\left ( x,y \right )}$ przy ograniczeniu budżetowym $\dpi{150} \mathbf{12x+16y=1280}$ . (długie rachunki)

Rozwiązanie

W zadaniu naszą funkcją $\dpi{120} f\left ( x,y \right )$ jest funkcja użyteczności $\dpi{120} u\left ( x,y \right )=x^{\frac{3}{4}}\cdot y^{\frac{1}{4}}$ , zaś funkcja $\dpi{120} g\left ( x,y \right )$ jest równa $\dpi{120} g\left ( x,y \right )=12x+16y-1280$ .

Tworzymy funkcję $\dpi{120} L\left ( x,y,\lambda \right )$ :

$\dpi{120} L\left ( x,y,\lambda \right )=u\left ( x,y \right )+\lambda \cdot g\left ( x,y \right )$

$\dpi{120} L\left ( x,y,\lambda \right )=x^{\frac{3}{4}}\cdot y^{\frac{1}{4}}+\lambda \cdot \left ( 12x+16y-1280 \right )$

Warunek konieczny

Liczymy pochodne cząstkowe:

$\dpi{120} L'_{x}=\frac{3}{4}x^{-\frac{1}{4}}\cdot y^{\frac{1}{4}}+12\lambda$

$\dpi{120} L'_{y}=\frac{1}{4}x^{\frac{3}{4}}\cdot y^{-\frac{3}{4}}+16\lambda$

$\dpi{120} L'_{\lambda }=12x+16y-1280$

Przyrównujemy pochodne cząstkowe do zera:

$\dpi{120} \left\{\begin{matrix} \frac{3}{4}x^{-\frac{1}{4}}\cdot y^{\frac{1}{4}}+12\lambda=0 \\ \frac{1}{4}x^{\frac{3}{4}}\cdot y^{-\frac{3}{4}}+16\lambda =0 \\ 12x+16y-1280=0\end{matrix}\right.$

Wyznaczamy z równań zmienną $\dpi{120} \lambda$ :

$\dpi{120} \left\{\begin{matrix} \lambda =-\frac{1}{16}x^{-\frac{1}{4}}\cdot y^{\frac{1}{4}}\; \; \; \; \; \; \\\lambda =- \frac{1}{64}x^{\frac{3}{4}}\cdot y^{-\frac{3}{4}} \; \; \; \; \; \; \\ 12x+16y-1280=0\end{matrix}\right.$

Porównujemy $\dpi{120} \lambda$ :

$\dpi{120} -\frac{1}{16}x^{-\frac{1}{4}}\cdot y^{\frac{1}{4}}=- \frac{1}{64}x^{\frac{3}{4}}\cdot y^{-\frac{3}{4}}/\cdot \left (-16 \right )$

$\dpi{120} 4x^{-\frac{1}{4}}\cdot y^{\frac{1}{4}}=x^{\frac{3}{4}}\cdot y^{-\frac{3}{4}}/\cdot x^{\frac{1}{4}} \cdot y^{\frac{3}{4}}$

$\dpi{120} 4y=x$

Wstawiamy do trzeciego równania:

$\dpi{120} 12\cdot 4y+16y-1280=0/:16$

$\dpi{120} 3y+y-80=0$

$\dpi{120} 4y=80/:4$

$\dpi{120} y=20$

Stąd:

$\dpi{120} \left\{\begin{matrix} \lambda =-\frac{1}{16}\cdot 80^{-\frac{1}{4}}\cdot 20^{\frac{1}{4}}\\ x=80\; \;\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \\ y=20\; \;\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \end{matrix}\right.$

$\dpi{120} \left\{\begin{matrix} \lambda =-\frac{\sqrt{2}}{32}\\ x=80 \; \; \; \\ y=20\; \; \; \end{matrix}\right.$

Mamy zatem jeden punkt stacjonarny $\dpi{120} \left ( x,y,\lambda \right )=\left (80,20,-\frac{\sqrt{2}}{32} \right )$ . Jak się za chwilę okaże liczenie konkretnej wartości $\dpi{120} \lambda$ nie jest konieczne.

Warunek dostateczny

Badamy znak tzw. Hesjanu obrzeżonego:

$\dpi{120} \left |\bar{H } \right |=\begin{vmatrix} 0 & g'_{x} & g'_{y}\\ g'_{x}& L''_{xx}& L''_{xy}\\ g'_{y}&L''_{yx} & L''_{yy} \end{vmatrix}.$

Liczymy potrzebne pochodne cząstkowe:

$\dpi{120} g'_{x}=12$ , $\dpi{120} g'_{y}=16$

$\dpi{120} L''_{xx}=-\frac{3}{16}x^{-\frac{5}{4}}\cdot y^{\frac{1}{4}}$ , $\dpi{120} L''_{xy}=\frac{3}{16}x^{-\frac{1}{4}}\cdot y^{-\frac{3}{4}}$

$\dpi{120} L''_{yx}=\frac{3}{16}x^{-\frac{1}{4}}\cdot y^{-\frac{3}{4}}$ , $\dpi{120} L''_{yy}=-\frac{3}{16}x^{\frac{3}{4}}\cdot y^{-\frac{7}{4}}$

Liczymy wartości pochodnych w punkcie stacjonarnym:

$\dpi{120} g'_{x}=12$ , $\dpi{120} g'_{y}=16$

$\dpi{120} L''_{xx}\left ( 80,20 \right )=-\frac{3}{16}\cdot 80^{-\frac{5}{4}}\cdot 20^{\frac{1}{4}}=-\frac{3}{16}\cdot \frac{\sqrt[4]{20}}{\sqrt[4]{80^{5}}}=-\frac{3\sqrt{2}}{2560}$ ,

$\dpi{120} L''_{xy}\left ( 80,20 \right )=L''_{yx}\left ( 80,20 \right )=\frac{3}{16}\cdot 80^{-\frac{1}{4}}\cdot 20^{-\frac{3}{4}}=\frac{3}{16}\cdot \frac{1}{\sqrt[4]{80}}\cdot \frac{1}{\sqrt[4]{20^{3}}}=\frac{3\sqrt{2}}{640}$ ,

$\dpi{120} L''_{yy}\left ( 80,20 \right )=-\frac{3}{16}\cdot 80^{\frac{3}{4}}\cdot 20^{-\frac{7}{4}}=-\frac{3}{16}\cdot \frac{\sqrt[4]{80^{3}}}{\sqrt[4]{20^{7}}}=-\frac{3\sqrt{2}}{160}$

Wstawiamy je do Hesjanu obrzeżonego:

$\dpi{120} \left |\bar{H } \right |=\begin{vmatrix} 0 & 12 & 16\\ 12& -\frac{3\sqrt{2}}{2560}& \frac{3\sqrt{2}}{640}\\ 16&\frac{3\sqrt{2}}{640} & -\frac{3\sqrt{2}}{160} \end{vmatrix}\begin{matrix} 0 & 12\\ 12 &-\frac{3\sqrt{2}}{2560} \\ 16& \frac{3\sqrt{2}}{640} \end{matrix}$

Pamiętajmy, że interesuje nas tylko znak Hesjanu, a nie jego konkretna wartość. Ponieważ tutaj mamy bardzo niewygodne liczby, zauważamy, że $\dpi{120} \left | \bar{H} \right |>0$ . (Kto ma cierpliwość liczy i otrzymuje wartość $\dpi{120} \frac{48\sqrt{2}}{10}$ )

Ponieważ wartość Hesjanu obrzeżonego jest dodatnia, zatem w punkcie $\dpi{120} \left ( 80,20 \right )$ funkcja $\dpi{120} u\left ( x,y \right )=x^{\frac{3}{4}}\cdot y^{\frac{1}{4}}$ osiąga maksimum warunkowe przy warunku $\dpi{120} 12x+16y-1280=0$ .

Pokaż rozwiązanie

Zwiń

Zadanie 5. Wzgórze ma kształt stożka, który w układzie $X Y Z $ ma równanie $\dpi{150} \mathbf{z=4-\sqrt{x^{2}+y^{2}}}$ $z = 4 - \sqrt{x^{2} + y^{2}} . $ Turysta porusza się po zboczu wzgórza w ten sposób, że rzut jego trasy na płaszczyznę $X Y $ jest prostą o równaniu $\dpi{150} \mathbf{y=x+1}$ $y = x + 1. $ Wyznacz współrzędne najwyżej położonego punktu trasy turysty.

Rozwiązanie

Zadanie to dla odmiany rozwiążemy bez mnożników Lagrange’a, ale oczywiście można wykorzystać również tą metodę.

Wzgórze ma kształt stożka opisanego równaniem $\dpi{120} z=4-\sqrt{x^{2}+y^{2}}$ . Jest to nasza funkcja $\dpi{120} f\left ( x,y \right )$ . Funkcja ta jest określona na całej płaszczyźnie $X Y . $ Jednak z warunków zadania wynika, że rozważamy ją w kole $\dpi{120} x^{2}+y^{2}\leqslant 16$ $x^{2} + y^{2} \leq 16 $ , ponieważ tylko tam przyjmuje ona wartości nieujemne. (nie będzie to miało wpływu na rachunki, ale dla poprawności zadania takie zastrzeżenie powinno się pojawić)

Zadanie sprowadza się do wyznaczenia punktu $\dpi{120} \left ( x_{0},y_{0} \right )$ $(x_{0}, y_{0}) $ , w którym funkcja $\dpi{120} f\left ( x,y \right )$ $f $ przyjmuje największą wartość przy warunku $\dpi{120} y=x+1$ $y = x + 1. $

Podstawiając $\dpi{120} y=x+1$ $y = x + 1 $ do wzoru funkcji $\dpi{120} f\left ( x,y \right )=4-\sqrt{x^{2}+y^{2}}$ $f, $ otrzymujemy funkcję jednej zmiennej $g (x) = f (x, x + 1) . $ Mamy:

$\dpi{120} h\left ( x \right )=f\left ( x,x+1 \right )=4-\sqrt{x^{2}+\left ( x+1 \right )^{2}}=4-\sqrt{2x^{2}+2x+1}$

Szukamy ekstremum funkcji $\dpi{120} h\left ( x \right )$ , tak jak zwykłego ekstremum lokalnego funkcji jednej zmiennej. Warunkiem koniecznym było zerowanie się pierwszej pochodnej. Mamy:

$\dpi{120} h'\left ( x \right )=-\frac{1}{2\sqrt{2x^{2}+2x+1}}\cdot \left ( 4x+2 \right )$

Po skróceniu:

$\dpi{120} h'\left ( x \right )=-\frac{2x+1}{\sqrt{2x^{2}+2x+1}}$

Przyrównujemy do zera i szukamy punktów podejrzanych o ekstremum (punktów stacjonarnych):

$\dpi{120} -\frac{2x+1}{\sqrt{2x^{2}+2x+1}}=0/\cdot \left ( - \sqrt{2x^{2}+2x+1}\right )$

$\dpi{120} 2x+1=0$

$\dpi{120} x=-\frac{1}{2}$

Jedynym punktem stacjonarnym jest punkt:

$\dpi{120} \left ( x_{0},y_{0} \right )=\left ( x_{0},x_{0}+1 \right )=\left ( -\frac{1}{2},-\frac{1}{2}+1 \right )=\left ( -\frac{1}{2},\frac{1}{2} \right )$ .

Warunkiem dostatecznym istnienia ekstremum lokalnego jest zmiana znaku pierwszej pochodnej. Robimy wykres znaku pochodnej. Pamiętajmy o minusie stojącym na początku wyrażenia. Zatem:

W punkcie $\dpi{120} x_{0}=-\frac{1}{2}$ wyrażenie $\dpi{120} y=-x-1$ $- 2 x - 1 $ zmienia znak z dodatniego na ujemny. Zatem funkcja $\dpi{120} h\left ( x \right )$ $g $ ma w punkcie $\dpi{120} x_{0}=-\frac{1}{2}$ maksimum lokalne.

Zatem w punkcie $\dpi{120} \left ( -\frac{1}{2},\frac{1}{2} \right )$ funkcja $\dpi{120} f\left ( x,y \right )=4-\sqrt{x^{2}+y^{2}}$ osiąga maksimum przy warunku $\dpi{120} y=x+1$ . Punkt $\dpi{120} \left ( -\frac{1}{2},\frac{1}{2} \right )$ należy do koła $\dpi{120} x^{2}+y^{2}\leqslant 16$ . Jest ono równe:

$\dpi{120} f_{max}\left ( -\frac{1}{2},\frac{1}{2} \right )=4-\sqrt{\left ( -\frac{1}{2} \right )^{2}+\left ( \frac{1}{2} \right )^{2}}=4-\sqrt{\frac{1}{2}}$

Współrzędne najwyżej położonego punktu: $\dpi{120} \left ( -\frac{1}{2},\frac{1}{2},4-\frac{1}{\sqrt{2}} \right )$ .

Pokaż rozwiązanie

Zwiń