Mamy 4 zadania. W pierwszym liczymy ekstrema różnych funkcji według schematu podanego w zakładce Wzory tutaj. Jest to najbardziej powszechne zadanie na kolokwiach. Zadania pozostałe są zadaniami z treścią. Zadanie 3 jest najtrudniejsze i najdłuższe, ale zachęcam do przestudiowania go.
Zadanie 1. Znaleźć ekstrema lokalne funkcji:
1)
Rozwiązanie
Krok 1.
Dziedzina funkcji: .
Liczymy pochodną:
Szukamy miejsc zerowych pochodnej:
– pierwiastek dwukrotny
Są to tzw. punkty podejrzane o ekstrema (punkty stacjonarne).
Krok 2.
Badamy znak pochodnej. Ponieważ , więc wszystko zależy od czynnika
.
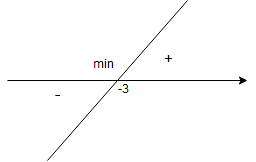
Zatem:
– dla
– dla
.
Krok 3.
Ponieważ w punkcie pochodna zmieniła znak z ”-” na ”+”, więc w tym punkcie mamy ekstremum lokalne i jest to minimum lokalne (tw. 2 zakładka Teoria). Liczymy jego wartość (wstawiamy
do wzoru
):
2)
Rozwiązanie
Krok 1.
Dziedzina funkcji: .
Liczymy pochodną:
Szukamy miejsc zerowych pochodnej:
,
.
Są to tzw. punkty podejrzane o ekstrema (punkty stacjonarne).
Krok 2.
Badamy znak pochodnej. Ponieważ , więc wszystko zależy od licznika
.
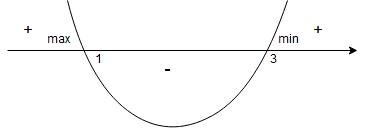
Zatem:
– dla
– dla
.
Krok 3.
W punkcie pochodna zmienia znak z ”+” na ”-”, więc jest to maksimum lokalne.
W punkcie pochodna zmienia znak z ”-” na ”+”, więc jest to minimum lokalne.
Liczymy wartości tych ekstremów:
3)
Rozwiązanie
Krok 1.
Dziedzina funkcji: .
Liczymy pochodną:
Szukamy miejsc zerowych pochodnej:
– pierwiastek dwukrotny
Są to tzw. punkty podejrzane o ekstrema (punkty stacjonarne).
Krok 2.
Badamy znak pochodnej. Ponieważ , więc wszystko zależy od czynnika
.
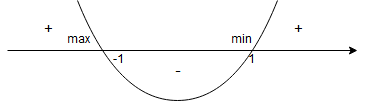
Zatem:
– dla
– dla
.
Krok 3.
W punkcie pochodna zmienia znak z ”+” na ”-”, więc jest to maksimum lokalne.
W punkcie pochodna zmienia znak z ”-” na ”+”, więc jest to minimum lokalne.
Liczymy wartości tych ekstremów:
4)
Rozwiązanie
Krok 1.
Dziedzina funkcji: . Stąd:
.
Liczymy pochodną:
Szukamy miejsc zerowych pochodnej:
Są to tzw. punkty podejrzane o ekstrema (punkty stacjonarne).
Krok 2.
Badamy znak pochodnej. Ponieważ , więc wszystko zależy od licznika
.
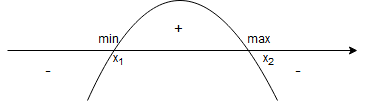
Zatem po uwzględnieniu dziedziny:
– dla
– dla
.
Krok 3.
W punkcie pochodna zmienia znak z ”-” na ”+”, więc jest to minimum lokalne.
W punkcie pochodna zmienia znak z ”+” na ”-”, więc jest to maksimum lokalne.
Liczymy wartości tych ekstremów:
5)
Rozwiązanie
Krok 1.
Dziedzina funkcji: .
Liczymy pochodną:
Szukamy miejsc zerowych pochodnej:
Jest to tzw. punkt podejrzany o ekstremum (punkt stacjonarny).
Krok 2.
Badamy znak pochodnej. Ponieważ , więc znak zależy od
.
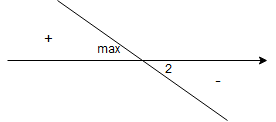
Zatem:
– dla
– dla
.
Krok 3.
W punkcie pochodna zmienia znak z ”+” na ”-”, więc jest to maksimum lokalne.
Liczymy wartość tego ekstremum:
6)
Rozwiązanie
Krok 1.
Dziedzina funkcji: .
Liczymy pochodną:
Szukamy miejsc zerowych pochodnej:
Są to tzw. punkty podejrzane o ekstrema (punkty stacjonarne).
Krok 2.
Badamy znak pochodnej. Ponieważ , więc znak zależy od
.

Zatem:
– dla
– dla
.
Krok 3.
W punkcie pochodna zmienia znak z ”-” na ”+”, więc jest to minimum lokalne.
W punkcie pochodna zmienia znak z ”+” na ”-”, więc jest to maksimum lokalne.
Liczymy wartości tych ekstremów:
7)
Rozwiązanie
Krok 1.
Dziedzina funkcji: . (dziedziną logarytmu jest
)
Liczymy pochodną:
Szukamy miejsc zerowych pochodnej:
Jest to tzw. punkt podejrzany o ekstremum (punkt stacjonarny).
Krok 2.
Badamy znak pochodnej. Ponieważ (uwzględniamy dziedzinę), więc znak zależy od
.
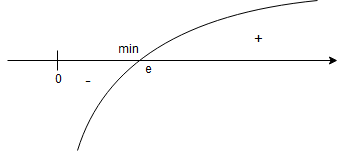
Zatem:
– dla
– dla
.
Krok 3.
W punkcie pochodna zmienia znak z ”-” na ”+”, więc jest to minimum lokalne.
Liczymy wartość tego ekstremum:
8)
Rozwiązanie
Krok 1.
Dziedzina funkcji: .
Liczymy pochodną:
Szukamy miejsc zerowych pochodnej:
Jest to tzw. punkt podejrzany o ekstremum (punkt stacjonarny).
Krok 2.
Badamy znak pochodnej. Ponieważ , więc znak zależy od
.

Zatem:
– dla
– dla
.
Krok 3.
W punkcie pochodna zmienia znak z ”-” na ”+”, więc jest to minimum lokalne.
Liczymy wartość tego ekstremum:
9)
Rozwiązanie
Krok 1.
Dziedzina funkcji: .
Liczymy pochodną:
Szukamy miejsc zerowych pochodnej:
Jest to tzw. punkt podejrzany o ekstremum (punkt stacjonarny).
Krok 2.
Badamy znak pochodnej.
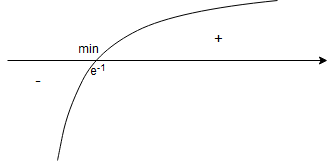
Mamy:
– dla
– dla
.
Krok 3.
W punkcie pochodna zmienia znak z ”-” na ”+”, więc jest to minimum lokalne.
Liczymy wartość tego ekstremum:
10)
Rozwiązanie
Krok 1.
Dziedzina funkcji: .
Liczymy pochodną:
Zauważmy, że pochodna nie posiada miejsc zerowych, więc funkcja nie ma ekstremów lokalnych.
Zadanie 2. Znaleźć współczynniki trójmianu takie, aby w punkcie
trójmian osiągał minimum równe
.
Rozwiązanie Aby trójmian miał jakiekolwiek ekstremum, musi być spełniony warunek konieczny istnienia ekstremum, czyli Ekstremum to ma być osiągnięte w punkcie Jest to minimum lokalne, gdyż pochodna w tym punkcie zmienia znak z ”-” na ”+” (funkcja liniowa rosnąca). Następnie wykorzystujemy fakt, iż to minimum ma w punkcie Ostatecznie otrzymujemy postać trójmianu:. Zatem:
więc:
.
osiągać wartość
. Zatem:
Zadanie 3. Znaleźć współczynniki wielomianu takie, aby w punkcie
wielomian osiągał maksimum równe
, a w punkcie
wielomian osiągał minimum równe
.
Rozwiązanie Warunek konieczny istnienia ekstremum Wiemy, że ekstrema mają być osiągnięte w punktach Następnie wiemy, że w punkcie Powstał układ czterech równań z czterema niewiadomymi: Układ ten można rozwiązywać różnymi metodami np. metodą wyznacznikową. My spróbujmy inaczej (nie chce nam się liczyć wyznaczników 4 stopnia). Odejmijmy czwarty wiersz od trzeciego. Mamy: Liczymy wyznaczniki: Zatem: Wstawiamy te wartości np. do trzeciego równania i otrzymujemy wartość parametru Otrzymaliśmy zatem wielomian: W punkcie .
oraz
. Zatem dostajemy układ równań:
wartość tego ekstremum wynosi
, zaś w punkcie
mamy wartość
. Dostajemy kolejne dwa równania:
.
,
,
,
,
,
.
:
jest rzeczywiście maksimum, a w punkcie
minimum. Wystarczy spojrzeć na pochodną i jej zmianę znaków w tych punktach.
Zadanie 4. Wydajność pracy jednego robotnika zmienia się w ciągu ośmiogodzinnego dnia pracy i po godzinach osiąga wartość
. W której godzinie pracy jego wydajność jest największa, jeśli rozpoczyna pracę o godzinie siódmej rano?
Rozwiązanie Liczymy pochodną funkcji Warunek konieczny istnienia ekstremum W zadaniu pytają o największą wydajność, czyli maksimum lokalne. Pochodna zmienia znak z ”+” na ”-” w punkcie A więc, największą wydajność robotnik osiągnie w trzeciej godzinie swojej pracy. Ponieważ rozpoczyna pracę o godzinie 7 rano, zatem największą wydajność osiągnie o godzinie 10 rano. .
.
, czyli:
,
,
.
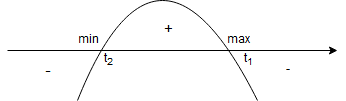
.